Circumraggio
In geometria, il circumraggio è il raggio del circumcerchio di un triangolo, pari alla distanza che separa il circocentro da uno qualsiasi dei suoi vertici.
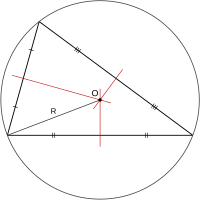
Più in generale tale nome può designare anche il raggio della circonferenza circoscritta a un poligono ciclico qualsiasi, o della sfera circoscritta ad alcuni poliedri.
Nel triangolo
modificaLa lunghezza del circumraggio è data dalla seguente relazione:
dove sono i lati del triangolo e è la sua area, che può essere calcolata con la formula di Erone.
Dimostrazione
modificaSia l'altezza relativa ad e
Si ricordi inoltre che
Sia il diametro della circonferenza circoscritta al triangolo passante per . I triangoli e sono simili quindi vale la relazione
ossia
e dividendo per 2 ambo i membri segue la tesi.
Esempi
modificaNel triangolo rettangolo, essendo il circocentro il punto medio dell'ipotenusa , il circumraggio è uguale alla metà di questa
Nel triangolo equilatero si ha
Relazioni con l'inraggio
modificaIl circumraggio è in stretta relazione con l'inraggio , il raggio della circonferenza inscritta, e con il semiperimetro:
Inoltre utilizzando il teorema dei seni si ha:
Nei poligoni in generale
modificaNei quadrilateri ciclici in generale la formula è
invece per un poligono regolare di lati di lunghezza è
qui denota la funzione cosecante.
Voci correlate
modificaCollegamenti esterni
modifica- (EN) Eric W. Weisstein, Circumraggio, su MathWorld, Wolfram Research.