Icosidodecadodecaedro camuso

In geometria, l'icosidodecadodecaedro camuso è un poliedro stellato uniforme avente 104 facce - 80 triangolari, 12 pentagonali e 12 a forma di pentagramma - 150 spigoli e 60 vertici.

Icosidodecadodecaedro camuso
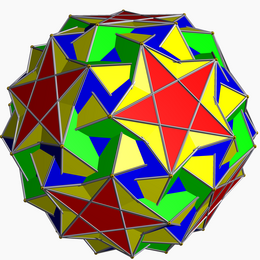Tipo	Poliedro stellato uniforme
Forma facce	20+60 triangoli 12 pentagoni 12 pentagrammi
Nº facce	104
Nº spigoli	180
Nº vertici	60
Caratteristica di Eulero	-16
Incidenza dei vertici	3.3.3.5.3.5/3
Notazione di Wythoff	| 5/3 3 5
Diagramma di Coxeter-Dynkin
Gruppo di simmetria	I, [5,3]+, 532
Duale	Esacontaedro esagonale medio
Proprietà	Non convessità
Politopi correlati
Figura al vertice Poliedro duale

Coordinate cartesiane

Le coordinate cartesiane per i vertici dell'icosidodecadodecaedro camuso, spesso indicato con il simbolo U₄₆ e il cui inviluppo convesso è un dodecaedro camuso non uniforme, sono date da tutte le permutazioni pari di:

$\left(\,\pm 2\alpha ,\,\pm 2\gamma ,\,\pm 2\beta \,\right)$

$\left(\,\pm (\alpha +\beta \varphi ^{-1}+\gamma \varphi ),\,\pm (-\alpha \varphi +\beta +\gamma \varphi ^{-1}),\,\pm (\alpha \varphi ^{-1}+\beta \varphi -\gamma )\,\right)$

$\left(\,\pm (-\alpha \varphi ^{-1}+\beta \varphi +\gamma ),\,\pm (-\alpha +\beta \varphi ^{-1}-\gamma \varphi ),\,\pm (\alpha \varphi +\beta -\gamma \varphi ^{-1})\,\right)$

$\left(\,\pm (-\alpha \varphi ^{-1}+\beta \varphi -\gamma ),\,\pm (\alpha -\beta \varphi ^{-1}-\gamma \varphi ),\,\pm (\alpha \varphi +\beta +\gamma \varphi ^{-1})\,\right)$

$\left(\,\pm (\alpha +\beta \varphi ^{-1}-\gamma \varphi ),\,\pm (\alpha \varphi -\beta +\gamma \varphi ^{-1}),\,\pm (\alpha \varphi ^{-1}+\beta \varphi +\gamma )\,\right)$

con un numero pari di segni più, dove $\varphi ={\tfrac {1+{\sqrt {5}}}{2}}$ è la sezione aurea, $\rho \approx 1,324718$ è il numero plastico, ossia l'unica soluzione reale dell'equazione $x^{3}=x+1$, e

$\alpha =\rho +1=\rho ^{3}\approx 2,324718$

$\beta =\varphi ^{2}\rho ^{4}+\varphi \approx 9,680520$

$\gamma =\rho ^{2}+\varphi \rho \approx 3,898317$

Poliedri correlati

Esacontaedro esagonale medio

Esacontaedro esagonale medio
Tipo	Poliedro stellato
Forma facce	Esagoni irregolari
Nº facce	60
Nº spigoli	180
Nº vertici	104
Caratteristica di Eulero	-16
Gruppo di simmetria	I, [5,3]+, 532
Duale	Icosidodecadodecaedro camuso

L'esacontaedro esagonale medio è un poliedro stellato isoedro, nonché il duale dell'icosidodecadodecaedro camuso, avente per facce 60 esagoni irregolari.

Dato un icosidodecadodecaedro camuso di spigolo pari a 1, immaginando l'esacontaedro esagonale medio come composto da 60 facce intersecanti a forma di esagono irregolare, come riportato nella figura sottostante, di cui solo una parte visibile all'esterno del solido, e considerando la già citata sezione aurea, il già citato numero plastico e il numero $\xi =-1/(2\rho )$, ogni faccia risulta avere quattro angoli uguali di ampiezza pari a $\arccos(\xi )\approx 112,175\,128\,045\,27^{\circ }$, uno ampio $\arccos(\phi ^{2}\xi +\phi )\approx 50,958\,265\,917\,31^{\circ }$ e uno ampio $360^{\circ }-\arccos(\phi ^{-2}\xi -\phi ^{-1})\approx 220,341\,221\,901\,59^{\circ }$, con due lati corti di lunghezza pari a $1-{\sqrt {(1-\xi )/(\phi ^{3}-\xi )}}\approx 0,453\,587\,559\,98$, due più grandi di lunghezza pari a $1+{\sqrt {(1-\xi )/(-\phi ^{-3}-\xi )}}\approx 4,121\,448\,816\,41$ e due medi di lunghezza pari a 2.

Collegamenti esterni

• (EN) Eric W. Weisstein, Snub Icosidodecadodecahedron, su MathWorld, Wolfram Research.
• (EN) Eric W. Weisstein, Esacontaedro esagonale medio, in MathWorld, Wolfram Research. URL consultato il 20 marzo 2024.