Espansione post-minkowskiana

Nell'ambito della teoria generale della relatività, le espansioni post-minkowskiane (PM) o approssimazioni post-minkowskiane sono metodi matematici utilizzati per trovare soluzioni approssimate delle equazioni di Einstein, mediante uno sviluppo in serie di potenze del tensore metrico.

Rapporto tra approssimazione post-minowskiana e post- newtoniana

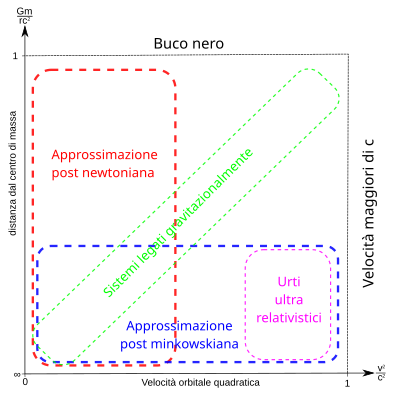
A differenza delle espansioni post-newtoniane (PN), in cui lo sviluppo in serie è basato su una combinazione di potenze della velocità (che deve essere trascurabile rispetto a quella della luce) e della costante gravitazionale, nel caso post-minkowskiano gli sviluppi sono basati soltanto sulla costante gravitazionale, consentendo l'analisi anche a velocità prossime a quella della luce (relativistiche).

	0PN		1PN		2PN		3PN		4PN		5PN		6PN		7PN
1PM	( 1	+	$v^{2}$	+	$v^{4}$	+	$v^{6}$	+	$v^{8}$	+	$v^{10}$	+	$v^{12}$	+	$v^{14}$	+	...)	$G^{1}$
2PM			( 1	+	$v^{2}$	+	$v^{4}$	+	$v^{6}$	+	$v^{8}$	+	$v^{10}$	+	$v^{12}$	+	...)	$G^{2}$
3PM					( 1	+	$v^{2}$	+	$v^{4}$	+	$v^{6}$	+	$v^{8}$	+	$v^{10}$	+	...)	$G^{3}$
4PM							( 1	+	$v^{2}$	+	$v^{4}$	+	$v^{6}$	+	$v^{8}$	+	...)	$G^{4}$
5PM									( 1	+	$v^{2}$	+	$v^{4}$	+	$v^{6}$	+	...)	$G^{5}$
6PM											( 1	+	$v^{2}$	+	$v^{4}$	+	...)	$G^{6}$
Tabella di confronto delle potenze utilizzate per le approssimazioni PN e PM nel caso di due corpi non rotanti. 0PN corrisponde al caso della teoria della gravitazione di Newton. 0PM (non riportato) corrisponde allo spazio piatto di Minkowsky.

Uno dei primi lavori su questo metodo di risoluzione è quello di Bruno Bertotti, pubblicato sul Nuovo Cimento nel 1956.

Voci correlate

• Approssimazione per i campi gravitazionali deboli
• Espansione post-newtoniana
• Formalismo post-newtoniano parametrizzato