Fascio gaussiano

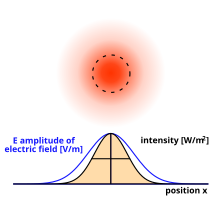
In ottica, un fascio di luce è detto gaussiano quando il suo profilo di intensità su un piano perpendicolare alla direzione di propagazione segue una distribuzione gaussiana. L'importanza nello studio dei fasci gaussiani sta nel fatto che ben descrivono, in termini ondulatori, la radiazione emessa da una sorgente laser; infatti molto spesso, specialmente nell'interazione con elementi ottici, l'approssimazione di considerare un fascio laser come un'onda piana non è valida.

Il profilo di intensità di dodici modi Hermite-Gaussiane

Derivazione dell'equazione d'onda per fasci gaussiani

Il punto di partenza sono ovviamente le equazioni di Maxwell dalle quali si ottiene, per il campo elettrico ad esempio, la nota equazione delle onde:

\nabla ^{2}{\vec {E}}-\mu \varepsilon {\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=0

Ponendo ${\vec {E}}(x,y,z,t)={\mbox{Re}}[{\vec {E}}(x,y,z)e^{i\omega t}]$ , che corrisponde a fissare la frequenza dell'onda elettromagnetica, si ottiene l'equazione di Helmholtz:

\nabla ^{2}{\vec {E}}+k^{2}(x,y,z){\vec {E}}=0

con $k^{2}(x,y,z)=\omega ^{2}\mu \varepsilon$ che in generale avrà una parte reale (responsabile della dispersione) ed una parte immaginaria (da cui originano l'assorbimento o l'amplificazione); per semplicità consideriamo il caso in cui $k^{2}$ non dipende dalle coordinate.

L'esperienza comune insegna che la radiazione laser si propaga come un'onda approssimativamente piana, per la quale il flusso di energia avviene in una particolare direzione z, con una simmetria cilindrica intorno a questa direzione e l'energia associata concentrata prevalentemente in una regione limitata attorno all'asse individuato da questa direzione. Questo suggerisce di cercare per una componente del vettore campo elettrico ortogonale a z, una soluzione dell'equazione di Helmholtz nella forma:

E(x,y,z)=\Psi (x,y,z)e^{-ikz}

\Psi (x,y,z)=e^{-i[P(z)+{\frac {1}{2}}Q(z)r^{2}]}

dove $r={\sqrt {x^{2}+y^{2}}}$ è la distanza dall'asse z. Tenendo conto della simmetria cilindrica del problema, è utile inoltre scrivere l'operatore laplaciano in questo modo

\nabla ^{2}=\nabla _{t}^{2}+{\frac {\partial ^{2}}{\partial z^{2}}}={\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial }{\partial r}}+{\frac {\partial ^{2}}{\partial z^{2}}}

in questa scrittura $\nabla _{t}^{2}$ ha quindi il significato di operatore laplaciano trasverso. L'equazione di Helmholtz è dunque

\nabla _{t}^{2}\Psi -2ik{\frac {\partial \Psi }{\partial z}}+{\frac {\partial ^{2}\Psi }{\partial z^{2}}}=0

Supponendo che la variazione lungo z sia sufficientemente bene descritta dalla sola derivata prima si può supporre che

{\frac {\partial ^{2}\Psi }{\partial z^{2}}}\ll k{\frac {\partial \Psi }{\partial z}},\;k^{2}\Psi

e quindi trascurare la derivata seconda nell'equazione. L'equazione per le funzioni $P(z)$ e $Q(z)$ diventa perciò

-Q^{2}r^{2}-2iQ-kr^{2}{\frac {dQ}{dz}}-2k{\frac {dP}{dz}}=0

Affinché questa sia vera per ogni r dovranno annullarsi identicamente i coefficienti delle diverse potenze di r; questo conduce al sistema

\left\{{\begin{matrix}Q^{2}+k{\frac {dQ}{dz}}=0\\{\frac {dP}{dz}}=-i{\frac {Q}{k}}\end{matrix}}\right.

Fasci gaussiani astigmatici

Il fascio gaussiano fondamentale $TEM_{00}$ si può pensare ottenuto a partire dal prodotto di due soluzioni dipendenti da $(x,z)$ e da $(y,z)$ con lo stesso spot-size di cintola. $V(x,y,z)=A{W_{0} \over W_{z}}e^{i\left(k_{z}-\phi _{z}\right)}e^{\left({ik \over 2R_{z}}-{1 \over W_{z}^{2}}\right)r^{2}}=TEM_{00}$ . Ci interessano ora dei fasci gaussiani il cui fattore gaussiano ha larghezza diversa su i due assi $x$ e $y$ . Ammettiamo inoltre che le posizioni delle cintole possano essere diverse. Questi prendono il nome di Fasci Gaussiani Astigmatici e la loro forma analitica, nel caso semplice in cui l'unica modulazione trasversale di ampiezza sia quella del fattore gaussiano, è la seguente: $V(x,y,z)=A{\sqrt {W_{0x}W_{0y} \over W_{x}(z)W_{y}(z)}}e^{i\left[k_{z}-{\phi _{x}(z)+\phi _{y}(z) \over 2}\right]}e^{\left({ik \over 2R_{x}(z)}-{1 \over W_{x}(z)^{2}}\right)x^{2}}e^{\left({ik \over 2R_{y}(z)}-{1 \over W_{y}(z)^{2}}\right)y^{2}}$ .

Soluzione dell'equazione d'onda

Il sistema di equazioni differenziali appena scritto è derivato da un'equazione approssimata, ma se ne può trovare una soluzione esatta; introducendo una nuova funzione incognita $s(z)$ definita da $Q(z)=k{\frac {s'}{s}}$ , dalla prima equazione si ha direttamente $s''(z)=0$ che si integra in maniera immediata. Quindi introducendo una costante di integrazione $q_{0}$

Q(z)={\frac {k}{z+q_{0}}}

Sostituendo questa nell'altra equazione si ottiene

P(z)=-i\ln \left(1+{\frac {z}{q_{0}}}\right)

La costante $q_{0}$ si può determinare osservando che se si vuole che l'ampiezza di $E$ decada allontanandosi dall'asse occorre avere $q_{0}$ immaginario puro; in genere si pone $q_{0}={\frac {i\pi {w_{0}}^{2}}{\lambda }}$ , con $\lambda ={\frac {2\pi }{k}}$ lunghezza d'onda della luce; $w_{0}$ ha le dimensioni di una lunghezza e il suo significato diverrà chiaro tra poco.

Finalmente l'espressione per il campo elettrico diventa

E(x,y,z)=E_{0}{\frac {w_{0}}{w(z)}}e^{-i\left(kz-\arctan \left({\frac {z}{z_{0}}}\right)\right)-r^{2}\left({\frac {1}{w^{2}(z)}}+{\frac {ik}{2R(z)}}\right)}

dove si sono definite le quantità

z_{0}={\frac {k{w_{0}}^{2}}{2}}\quad w^{2}(z)={w_{0}}^{2}\left(1+{\frac {z^{2}}{{z_{0}}^{2}}}\right)\quad R(z)=z\left(1+{\frac {{z_{0}}^{2}}{z^{2}}}\right)

mentre il parametro $q(z)$ definito da ${\frac {1}{q(z)}}={\frac {1}{R(z)}}-{\frac {2i}{kw^{2}(z)}}$ prende il nome di raggio di curvatura complesso, che contiene tutta l'informazione necessaria per lo studio della propagazione del fascio gaussiano.

La soluzione trovata prende il nome di fascio gaussiano fondamentale, per distinguerlo da altre soluzioni dette modi gaussiani di ordine superiore.

Intensità del fascio

L'intensità trasportata dal fascio gaussiano fondamentale mediata su un periodo $T={\frac {2\pi }{\omega }}$ è data da

I(x,y,z)={\frac {\pi c\varepsilon }{\lambda k}}E^{*}(x,y,z)E(x,y,z)=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}e^{\frac {-2r^{2}}{w^{2}(z)}}

Diametro del fascio

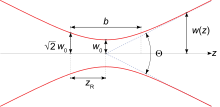
Il parametro $w(z)$ rappresenta la distanza dall'asse z alla quale l'ampiezza del campo si riduce di un fattore $1/e$ e l'intensità si riduce di $1/e^{2}$ ; in inglese prende il nome di spot size (letteralmente "dimensione del punto") del fascio. In pratica rappresenta la metà del diametro dell'area intorno all'asse di propagazione del fascio in cui è concentrata la maggior parte della potenza.

A questo punto appare chiaro il significato di $w_{0}$ , che rappresenta il minimo, per $z=0$ , delle dimensioni trasverse del fascio gaussiano, cioè per $z=0$ si ha il massimo di intensità. Il nome inglese è waist (letteralmente "cintura").

Parametro confocale

Per $z=\pm z_{0}$ la quantità $w(z)$ aumenta rispetto al minimo di un fattore ${\sqrt {2}}$ ; $z_{0}$ prende di solito il nome di distanza di Rayleigh, mentre il parametro confocale è pari a $2z_{0}$ . È quella distanza per cui il raggio ancora non si è allargato significativamente e l'intensità media è diminuita solo di un fattore 2. Quando si ha a che fare con un fascio laser, rappresenta la lunghezza di riferimento con cui confrontare le distanze focali di eventuali sistemi ottici attraversati.

Raggio di curvatura

Per $r^{2}\ll z^{2}$ il fronte d'onda di un fascio gaussiano può essere approssimato con un fronte d'onda sferico di raggio $R(z)$ . In $z=0$ diverge, cioè il fronte d'onda è piano, mentre in valore assoluto è minimo per $z=\pm z_{0}$ ; a grande distanza dal punto di waist si può considerare $R(z)\simeq z$ , cioè un'onda praticamente sferica.

Divergenza e fattore $M^{2}$

Anche $w(z)$ per $z\gg z_{0}$ cresce linearmente con $z$ ; l'angolo $\theta \simeq {\frac {\lambda }{\pi w_{0}}}$ formato tra l'asse z e la retta che approssima $w(z)$ prende il nome di divergenza angolare e si può dimostrare che un fascio gaussiano è quello che ha divergenza minima. In un laser reale la divergenza è sempre maggiore di questo valore limite, cioè il fascio generato da un laser reale non è mai esattamente gaussiano; nei laser per applicazioni scientifiche questo è espresso quantitativamente dal fattore $M^{2}$ , che rappresenta il rapporto tra la divergenza effettiva e quella ideale; in laser di qualità elevata $M^{2}$ può essere molto vicino a 1 e spesso dalle case costruttrici viene fornito un valore massimo garantito.

Propagazione di un fascio gaussiano attraverso un sistema ottico

Usando il formalismo dell'ottica matriciale, la propagazione di un fascio gaussiano è descritta da una trasformazione del raggio di curvatura complesso; se la matrice che descrive il sistema è

{\begin{pmatrix}A&B\\C&D\end{pmatrix}}

allora il raggio complesso all'uscita del sistema $q_{o}$ si ricava a partire da quello in ingresso $q_{i}$ semplicemente scrivendo

q_{o}={\frac {Aq_{i}+B}{Cq_{i}+D}}

oppure più convenientemente

{\frac {1}{q_{o}}}={\frac {C+D/q_{i}}{A+B/q_{i}}}

questa formula è nota con il nome di Legge ABCD dell'ottica dei fasci gaussiani. È facile dimostrare tramite questa legge che nell'attraversare una lente o un sistema di lenti un fascio gaussiano è trasformato in un altro fascio gaussiano con parametri $w_{0}$ e $z_{0}$ modificati.

Focalizzazione di un fascio gaussiano

Consideriamo un fascio gaussiano con distanza di Rayleigh $z_{0}$ che incide nel punto di waist su di una lente sottile convergente (focale $f$ positiva); il fascio gaussiano all'uscita dalla lente ha un punto di waist ad una distanza dalla lente data da

d={\frac {f}{1+\left({\frac {f}{z_{0}}}\right)^{2}}}

$d$ coincide con $f$ nell'ipotesi che $f\ll z_{0}$ ; inoltre, sempre in questa ipotesi di corta lunghezza focale, si ha che il nuovo waist è

w_{0o}=w_{0i}{\frac {\frac {f}{z_{0}}}{\sqrt {1+\left({\frac {f}{z_{0}}}\right)^{2}}}}\simeq {\frac {f}{z_{0}}}w_{0i}

Per focalizzare un fascio gaussiano occorrono quindi lenti di focale corta rispetto alla distanza di Rayleigh.

Bibliografia

Bahaa E. A. Saleh, Malvin Carl Teich, Fundamentals of Photonics, Second Edition, Wiley-Interscience, 2007. ISBN 9780471358329

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su Fascio gaussiano