Ippopede

Un ippopede è una curva piana che obbedisce alla seguente equazione in coordinate polari

Esempi di ippopede con a=1, b=0.1, 0.2, 0.5, 1.0, 1.5 e 2.0.

Esempi di ippopede con b=1, a=0.1, 0.2, 0.5, 1.0, 1.5 e 2.0.

$r^{2}=4b(a-b\sin ^{2}\theta )\,$

oppure a quella in coordinate cartesiane

$\left(x^{2}+y^{2}\right)^{2}+4b(b-a)(x^{2}+y^{2})=4b^{2}x^{2},$

dove a e b sono costanti positive.

Il termine "ippopede" significa letteralmente "piede di cavallo".

La curva è spesso chiamata con il nome di ippopede di Proclo, dato che Proclo fu il primo a studiarla, insieme a Eudosso (che la utilizzò nella sua teoria sul moto dei pianeti), o anche lemniscata di Booth in virtù del lavoro svolto su di essa da James Booth (1806-1878).

L'ippopede è la sezione spirica in cui il piano secante è tangente all'interno del toro.

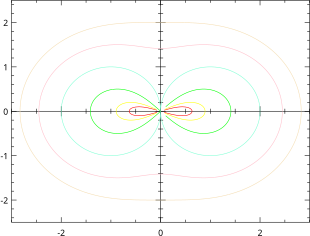
La curva assume diverse forme a seconda di dove il toro è sezionato. Può essere un semplice ovale, un ovale indentato o una lemniscata di Booth ellittica (0<b<a), due circonferenze isolate, oppure ancora una figura a otto o lemniscata di Booth iperbolica (0<a<b).

Nel caso particolare in cui $b=2a$, l'ippopede viene a coincidere con la lemniscata di Bernoulli.

Oltre che come sezione spirica, l'ippopede può essere anche vista come:

• la cissoide di due circonferenze di ugual raggio;
• una curva di Watt nella quale la lunghezza dell'asta e la distanza fra i centri delle due circonferenze sono uguali.

Bibliografia

• Lawrence JD. (1972) Catalog of Special Plane Curves, Dover. pp. 145–146.
• Booth J. A Treatise on Some New Geometrical Methods, Longmans, Green, Reader, and Dyer, London, Vol. I (1873) and Vol. II (1877).

Collegamenti esterni

• MathWorld description, su mathworld.wolfram.com.
• 2Dcurves.com description, su 2dcurves.com.
• www.daviddarling.info/encyclopedia/H/hippopede.html, su daviddarling.info.