Legge di Dulong-Petit

La legge di Dulong-Petit stabilisce che tutti gli elementi solidi hanno lo stesso valore del calore specifico molare.

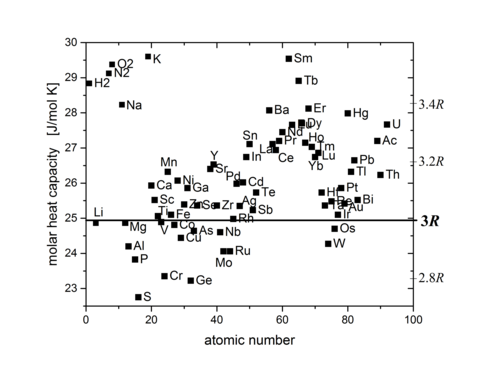
In termini moderni tale legge si esprime dicendo che il calore specifico di una mole degli elementi solidi è 3R, dove R è la costante dei gas. La teoria moderna del calore specifico dei solidi stabilisce che essa è dovuta alla termodinamica delle vibrazioni reticolari nel solido.

La figura a fianco mostra il valore del calore specifico molare sperimentale di gran parte degli elementi a temperatura ambiente.

Storia

Pierre Louis Dulong e Alexis Thérèse Petit trovarono sperimentalmente nel 1819 che il calore specifico per unità di massa di 13 elementi aveva un valore costante, se esso era moltiplicato per un numero che rappresentava il peso atomico dell'elemento. Jöns Jacob Berzelius aveva calcolato il valore del peso atomico degli elementi noti a quel tempo. Dulong e Petit non conoscevano la relazione con R, poiché questa costante non era stata ancora introdotta dalla teoria cinetica dei gas sviluppata successivamente. Il valore di 3R è circa 25 joule per kelvin, Dulong e Petit trovarono che questo era proprio il calore specifico molare.

Nel 1833 Amedeo Avogadro fece notare che la legge non si applicava su campioni di carbonio ^[1].

La legge di Kopp sviluppata nel 1865 da Hermann Franz Moritz Kopp ha esteso la legge di Dulong-Petit ai composti chimici sulla base di nuovi dati sperimentali.

Nel 1876 Heinrich Friedrich Weber notò che il calore specifico del diamante variava sensibilmente con la temperatura e fosse molto più basso di quanto previsto dalla legge di Dulong Petit^[1].

Nel 1877 Ludwig Boltzmann mostrò che la legge poteva essere spiegata in termini di oscillatori armonici classici ^[1]^[2]. Nel 1907 Albert Einstein ha esteso il modello agli oscillatori armonici quantistici per cercare di spiegare l'osservazione sperimentale della diminuzione con la temperatura del calore specifico del diamante.

Nel 1912 Peter Debye fece un nuovo modello, che è attualmente considerato valido, in cui le vibrazioni non sono oscillatori singoli, ma moti collettivi del reticolo ionico. Il modello di Debye permette di prevedere il calore specifico sia a temperature vicine allo zero assoluto che ad alta temperatura dove coincide con la legge di Dulong-Petit.

Il modello di Drude sviluppato nel 1900 sovrastimava il calore specifico dovuto al gas di elettroni classici, in base a tale modello vi dovrebbe essere un calore specifico molare molto maggiore nei conduttori rispetto agli isolanti. Solo nel 1927 con il modello di Sommerfeld, che tiene conto delle proprietà quantistiche degli elettroni nei metalli, si è capito come il contributo al calore specifico da parte del gas di elettroni sia trascurabile, spiegando quindi il risultato sperimentale che non vi è una differenza apparente nel calore specifico molare tra elementi solidi metallici o isolanti.

Modello

Il modello si basa sul fatto che la temperatura in un elemento solido, a livello microscopico, è determinata dall'ampiezza delle vibrazioni reticolari del solido. In particolare gli unici modi che sono eccitati all'equilibrio termodinamico sono quelli normali. Si chiamano modi normali quei modi di vibrazione che hanno una lunghezza d'onda sottomultiplo delle dimensioni fisiche del cristallo stesso. Infatti solo i modi normali non interferiscono distruttivamente. Questo vuole dire che se ho una mole, cioè un numero di Avogadro di atomi $N_{A}\$ , nel cristallo avrò la possibilità di $3N_{A}\$ modi normali (due onde trasversali ed una longitudinale). Tali modi hanno una energia cinetica e una energia potenziale in media di $k_{B}T/2\$ (a causa del teorema di equipartizione dell'energia), dove $k_{B}\$ è la costante di Boltzmann. Quindi l'energia interna di una mole, considerando tutti i modi normali, vale:

U=6N_{A}{\frac {k_{B}T}{2}}=3RT\

si è fatta la sostituzione di $N_{A}k_{B}$ con R.

La derivata dell'energia interna rispetto alla temperatura è il calore specifico molare^[3]:

c_{v}={\frac {\partial U}{\partial T}}=3R\approx 25\ {\frac {\mathrm {J} }{\mathrm {mol~K} }}

Il risultato della legge è che tale calore specifico sia una costante eguale per tutti gli elementi solidi. A temperatura ambiente la maggior parte dei solidi rispetta tale legge. Le uniche eccezioni sono alcuni elementi, molto duri, che hanno un calore specifico molare inferiore a quello previsto da tale legge, esempi di tali eccezioni sono il diamante e in misura minore il silicio. Notiamo sperimentalmente che a temperatura sufficientemente alta tutte le sostanze, compresi i tutti i solidi (anche il diamante), rispettano approssimativamente la legge di Dulong e Petit.

Note

^ ^a ^b ^c (EN) Carlo Cercignani, Ludwig Boltzmann: The Man Who Trusted Atoms, OUP Oxford, 12 gennaio 2006, ISBN 978-0-19-160698-4.
^ (EN) Steven H. Simon, The Oxford Solid State Basics, OUP Oxford, 20 giugno 2013, ISBN 978-0-19-968076-4.
^ Nicola Manini, Introduction to the Physics of Matter, Springer, 2014, ISBN 978-3-319-14381-1. p.237

Collegamenti esterni

(EN) Dulong–Petit law, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.

Controllo di autorità	GND (DE) 1191506096

Portale Termodinamica: accedi alle voci di Wikipedia che trattano di termodinamica

[:0-1] (EN) Carlo Cercignani, Ludwig Boltzmann: The Man Who Trusted Atoms, OUP Oxford, 12 gennaio 2006, ISBN 978-0-19-160698-4.

[2] (EN) Steven H. Simon, The Oxford Solid State Basics, OUP Oxford, 20 giugno 2013, ISBN 978-0-19-968076-4.

[3] Nicola Manini, Introduction to the Physics of Matter, Springer, 2014, ISBN 978-3-319-14381-1. p.237

[1]

[2]

[3]