Handshake (matematica)
Nella teoria dei grafi il lemma di handshaking è l'affermazione che ogni grafo non orientato finito ha un numero pari di vertici con grado dispari (il numero di archi che toccano il vertice). In termini più colloquiali, in un gruppo di persone alcune delle quali si stringono la mano, un numero pari di persone deve aver stretto la mano di un numero dispari di altre persone. I vertici di grado dispari in un grafo sono talvolta chiamati nodi dispari o vertici dispari; in questa terminologia, il lemma di handshaking può essere riformulato come l'affermazione che ogni grafo ha un numero pari di nodi dispari.
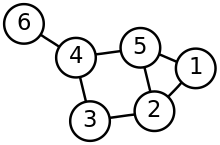
Il lemma di handshaking è una conseguenza della formula della somma dei gradi (a volte chiamato a sua volta lemma di handshaking),
per un grafo con insieme di vertici V e archi E. Entrambi i risultati furono provati da Leonhard Euler (1736) nel suo famoso articolo sui sette ponti di Königsberg che iniziò lo studio della teoria dei grafi.
Altre applicazioni includono la dimostrazione che per alcune strutture combinatorie, il numero di strutture è sempre pari, e l'assistenza con le prove del lemma di Sperner e del problema del "mountain climbing" (in italiano "alpinismo"). La classe di complessità PPA incapsula la difficoltà di trovare un secondo vertice dispari, dato uno di questi vertici in un grande grafo definito implicitamente.
Prova
modificaLa dimostrazione di Eulero della formula della somma dei gradi utilizza la tecnica del doppio conteggio : conta il numero di coppie incidenti (v , e) dove e è uno spigolo e il vertice v è uno dei suoi estremi, in due modi diversi. Il vertice v appartiene alle coppie deg (v), dove deg (v) (il grado di v) è il numero di archi ad esso incidenti. Pertanto, il numero di coppie incidenti è la somma dei gradi. Tuttavia, ogni arco nel grafico appartiene esattamente a due coppie incidenti, una per ciascuno dei suoi punti finali; pertanto, il numero di coppie incidenti è 2 | E|. Poiché queste due formule contano lo stesso insieme di oggetti, devono avere valori uguali.
In una somma di numeri interi, la parità della somma non è influenzata dai termini pari nella somma; la somma complessiva è pari quando c'è un numero pari di termini dispari e dispari quando c'è un numero dispari di termini dispari. Poiché un lato della formula della somma dei gradi è il numero pari 2 | E |, la somma sull'altro lato deve avere un numero pari di termini dispari; cioè, deve esserci un numero pari di vertici di grado dispari.
In alternativa, è possibile utilizzare l'induzione matematica per dimostrare che il numero di vertici di grado dispari è pari, rimuovendo un bordo alla volta da un dato grafo e utilizzando un'analisi del caso sui gradi dei suoi punti finali per determinare l'effetto di questo rimozione sulla parità del numero di vertici di grado dispari.
In classi speciali di grafici
modificaGrafici regolari
modificaLa formula della somma dei gradi implica che ogni r - grafo regolare con n vertici ha nr / 2 archi. In particolare, se r è dispari, il numero di archi deve essere divisibile per r e il numero di vertici deve essere pari.
Grafici infiniti
modificaUn grafico infinito che non obbedisce al lemma di handshaking. Il lemma di handshaking non si applica ai grafi infiniti, anche quando hanno solo un numero finito di vertici di grado dispari. Ad esempio, un grafo di percorso infinito con un punto finale ha solo un singolo vertice di grado dispari anziché avere un numero pari di tali vertici.
Applicazioni
modificaPercorsi e tour di Eulero
modificaLeonhard Euler ha dimostrato per la prima volta il lemma della stretta di mano nel suo lavoro sui sette ponti di Königsberg, chiedendo un tour a piedi della città di Königsberg (ora Kaliningrad) attraversando ciascuno dei suoi sette ponti una volta. Questo può essere tradotto in termini di teoria dei grafi come chiedere un percorso di Eulero o un tour di Eulerodi un grafo connesso che rappresenta la città e i suoi ponti: una passeggiata attraverso il grafo che attraversa ogni bordo una volta, terminando in un vertice diverso da quello che inizia nel caso di un percorso di Eulero o tornando al punto di partenza nel caso di un Eulero tour. Eulero ha affermato i risultati fondamentali di questo problema in termini di numero di vertici dispari nel grafo, che il lemma di handshaking limita ad essere un numero pari. Se questo numero è zero, esiste un percorso di Eulero e se è due, esiste un percorso di Eulero. In caso contrario, il problema non può essere risolto. Nel caso dei sette ponti di Königsberg, il grafo che rappresenta il problema ha quattro vertici dispari e non ha né un percorso di Eulero né un giro di Eulero.
In algoritmo Christofides-Serdyukov per approssimare il problema del commesso viaggiante, il fatto che il numero di vertici dispari è anche gioca un ruolo chiave, permettendo l'algoritmo per collegare tali vertici a coppie per costruire un grafico in cui un giro Eulero costituisce tour TSP approssimativo[1].
Nell'enumerazione combinatoria
modificaSi può dimostrare che diverse strutture combinatorie sono pari in numero collegandole ai vertici dispari in un appropriato "grafo di scambio".
Ad esempio, come dimostrato da CAB Smith, in qualsiasi grafo cubico G deve esserci un numero pari di cicli hamiltoniani attraverso un arco fisso uv; Thomason (1978) ha utilizzato una dimostrazione basata sul lemma di handshaking per estendere questo risultato ai grafi G in cui tutti i vertici hanno gradi dispari. Thomason definisce un grafo di scambio H, i cui vertici sono in corrispondenza uno-a-uno con i cammini hamiltoniani che iniziano in u e continuano per v. Due di tali percorsi p 1 e p 2 sono collegati da un bordo in Hse si può ottenere p 2 aggiungendo un nuovo bordo alla fine di p 1 e rimuovendo un altro bordo dalla metà di p 1; questa è una relazione simmetrica, quindi H è un grafo non orientato. Se il percorso p termina al vertice w, allora il vertice corrispondente a p in H ha grado uguale al numero di modi in cui p può essere esteso da un arco che non si ricollega a u; cioè, il grado di questo vertice in H è o deg (w) - 1 (un numero pari) se pnon fa parte di un ciclo hamiltoniano attraverso uv, o deg (w) - 2 (un numero dispari) se p fa parte di un ciclo hamiltoniano attraverso uv. Poiché H ha un numero pari di vertici dispari, G deve avere un numero pari di cicli hamiltoniani attraverso uv.
Altre applicazioni
modificaIl lemma di handshaking viene utilizzato anche nelle dimostrazioni del lemma di Sperner e del caso lineare a tratti del problema del "mountain climbing". Si tratta di trovare le condizioni che devono soddisfare due funzioni che formano i profili di una montagna bidimensionale, in modo che due climber (alpinisti in italiano) possano partire dal fondo sui lati opposti della montagna e coordinare i loro movimenti per incontrarsi (possibilmente in alto) rimanendo sempre alla stessa altezza.
Complessità computazionale
modificaIn connessione con il metodo del grafo di scambio per provare l'esistenza di strutture combinatorie, è interessante chiedersi quanto efficientemente queste strutture possano essere trovate. Ad esempio, si supponga di fornire come input un ciclo hamiltoniano in un grafo cubico; segue dal teorema di Smith che esiste un secondo ciclo. Quanto velocemente si può trovare questo secondo ciclo? Papadimitriou (1994) ha studiato la complessità computazionale di domande come questa, o più in generale della ricerca di un secondo vertice di grado dispari quando si è dato un singolo vertice dispari in un grande grafo definito implicitamente. Ha definito la classe di complessità PPA per incapsulare problemi come questo; una classe strettamente correlata definita su grafi diretti, PPAD, ha attirato un'attenzione significativa nella teoria dei giochi algoritmici perché calcolare un equilibrio di Nash è computazionalmente equivalente ai problemi più difficili in questa classe.
Note
modifica- ^ Nicos Christofides, Worst-case analysis of a new heuristic for the travelling salesman problem (PDF), Report 388, 1976. URL consultato il 4 febbraio 2021 (archiviato dall'url originale il 21 luglio 2019).. The handshaking lemma is cited at the top of page 2.
