Lemniscata di Bernoulli

In matematica, la lemniscata di Bernoulli è una curva algebrica piana a forma di otto orizzontale: essa è definita dai punti per i quali il prodotto delle distanze da due punti fissati detti fuochi è costante e uguale a $c^{2};$ è descritta in coordinate cartesiane nella forma:

Orbita del punto $P_{0}(x_{0},y_{0})=\left\{{\begin{matrix}x_{0}={\frac {2t+4t^{3}}{1+4t^{4}}}\\y_{0}={\frac {2t-4t^{3}}{1+4t^{4}}}\end{matrix}}\right.$ al variare del parametro $t$ in $\mathbb {R}$, le coordinate del punto sono una possibile rappresentazione parametrica della lemniscata di Bernoulli

Vari modi per la costruzione di lemniscate. Animazioni realizzate in MSWLogo

$(x^{2}+y^{2})^{2}=2c^{2}(x^{2}-y^{2}).$

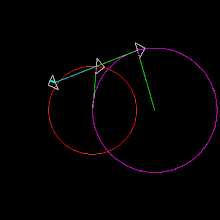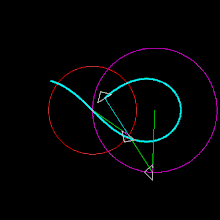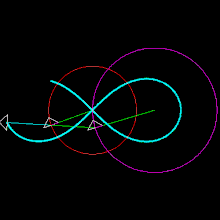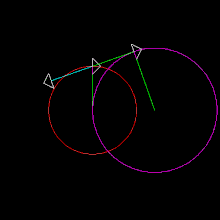
Il grafico di questa equazione produce una curva simile al simbolo dell'infinito $\infty$, che a sua volta è chiamato lemniscata. La rappresentazione Unicode di ∞ è (∞).

La lemniscata fu descritta per la prima volta nel 1694 da Jakob Bernoulli, come variante dell'ellisse, che è il luogo dei punti per i quali la somma delle distanze da due punti fissi detti fuochi è costante. Bernoulli la chiamò lemniscus, derivante dal greco λημνίσκος, lemníscos, che è l'equivalente latino di fiocco pendente.

La lemniscata era in effetti già stata trattata da Giovanni Cassini nel suo studio del 1680 sull'ovale di Cassini, di cui la lemniscata costituisce un caso particolare. Giovanni Fagnano dei Toschi nel 1750 ne studiò le principali proprietà.

Lunghezza

La lunghezza della lemniscata di Bernoulli i cui due punti più distanti dal centro si trovino sui punti $(-1,0)$ e $(1,0)$ è lunga approssimativamente 2,622. Questa grandezza, calcolata da Carl Gauss, è indicata con il simbolo $\varpi$. Il rapporto tra $\pi$ e $\varpi$ è uguale alla media aritmetico-geometrica tra 1 e ${\sqrt {2}}$. La dimostrazione di questa identità ha portato ad avanzamenti nelle tecniche di calcolo degli integrali ellittici.

Altre equazioni

La lemniscata di Bernoulli può anche essere descritta dalle equazioni polari

$r^{2}=2c^{2}\cos 2\theta$

o dall'equazione bipolare

$rr'=c^{2}.$

Bibliografia

• (EN) Lemniscate of Bernoulli, in The MacTutor History of Mathematics archive, School of Mathematics and Statistics, University of St Andrews, Scotland. URL consultato il 16 luglio 2008.
• (EN) J. Dennis Lawrence, A catalog of special plane curves, Dover Publications, 1972, pp. 4–5,121–123,145,151,184, ISBN 0-486-60288-5.

Voci correlate

• Lemniscata di Booth
• Lemniscata di Gerono
• Infinito (matematica)

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sulla lemniscata di Bernoulli

Collegamenti esterni

• Bernoulli, lemniscata di, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) lemniscate of Bernoulli, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Lemniscate, su MathWorld, Wolfram Research.
• (FR) Pagina sulla lemniscata di Bernoulli, su mathcurve.com.
• Lemniscata di Bernoulli come inviluppo di circonferenze, su webalice.it. URL consultato il 2 gennaio 2011 (archiviato dall'url originale il 9 aprile 2016).

Controllo di autorità	Thesaurus BNCF 36777