Quartile
In statistica, in particolare in statistica descrittiva, data una distribuzione di un carattere quantitativo oppure qualitativo ordinabile (ovvero le cui modalità possano essere ordinate in base a qualche criterio), i quartili sono quei valori/modalità che ripartiscono la popolazione in quattro parti di uguale numerosità.[1]
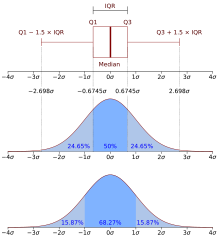
I quartili sono indici di posizione e rientrano nell'insieme delle statistiche d'ordine.
La differenza tra il terzo ed il primo quartile è un indice di dispersione ed è detto scarto interquartile; i quartili vengono inoltre utilizzati per rappresentare un box-plot.
Definizione
modificaIl quartile zero, il primo, il secondo, il terzo e il quarto quartile corrispondono con le prime modalità la cui frequenza cumulata percentuale è almeno 0, 25, 50, 75 e 100 rispettivamente. Cioè, ad esempio, il primo quartile corrisponde con la modalità i-esima se la frequenza cumulata percentuale e .
Il primo, il secondo e il terzo quartile in una distribuzione ordinata sono "vicini" ai valori di posizione [n/4], [n/2] e [3n/4].
Legami con altre statistiche d'ordine
modificaIl secondo quartile coincide con la mediana, e divide la popolazione in due parti di uguale numerosità, delle quali il primo ed il terzo quartile sono le mediane.
Il quartile zero coincide con il valore minimo della distribuzione. Il quarto quartile coincide con il valore massimo della distribuzione.
I quartili equivalgono ai quantili q0 (quartile zero), q1/4 (primo quartile), q2/4=q1/2 (secondo quartile), q3/4 (terzo quartile) e q1 (quarto quartile).
Esempio
modificaIn un sondaggio fatto all'interno di una facoltà composta da 250 studenti (la popolazione statistica), si intende rilevare il carattere "Gradimento dei professori", secondo le cinque modalità "molto deluso", "insoddisfatto", "parzialmente soddisfatto", "soddisfatto", "entusiasta". Risulta che 10 studenti si dicono entusiasti dell'operato dei professori, 51 si dicono soddisfatti, 63 mediamente soddisfatti, 90 insoddisfatti, 36 molto delusi.
La distribuzione di frequenza viene rappresentata con una tabella come la seguente:
| Gradimento dei professori | Frequenze assolute | Frequenze relative | Frequenze percentuali | Frequenze cumulate assolute | Frequenze cumulate relative | Frequenze cumulate percentuali |
|---|---|---|---|---|---|---|
| molto deluso | 36 | 0,144 | 14,4 | 36 | 0,144 | 14,4 |
| insoddisfatto | 90 | 0,360 | 36 | 126 | 0,504 | 50,4 |
| parzialmente soddisfatto | 63 | 0,252 | 25,2 | 189 | 0,756 | 75,6 |
| soddisfatto | 51 | 0,204 | 20,4 | 240 | 0,960 | 96 |
| entusiasta | 10 | 0,040 | 4 | 250 | 1,000 | 100 |
| Totali | 250 | 1,000 | 100 |
Nel caso ipotizzato, il primo quartile e la mediana sono rappresentati dalla modalità "insoddisfatto", mentre il terzo quartile è rappresentato dalla modalità "parzialmente soddisfatto". Questo significa che almeno la metà degli studenti non è soddisfatto dei professori e almeno tre quarti degli studenti non è pienamente soddisfatto.
Note
modifica- ^ Glossario Istat Archiviato il 31 dicembre 2011 in Internet Archive.
Bibliografia
modifica- G. Leti (1983): Statistica descrittiva, Bologna, Il Mulino, ISBN 88-15-00278-2.
Voci correlate
modificaCollegamenti esterni
modifica- quartile, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- quartile, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
- quartile, su sapere.it, De Agostini.
- quartile, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- quartile, in Dizionario di Economia e Finanza, Istituto dell'Enciclopedia Italiana, 2012.
- (EN) quartile, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Quartile, su MathWorld, Wolfram Research.