Modello logit

In statistica, il modello logit, noto anche come modello logistico o regressione logistica, è un modello di regressione nonlineare utilizzato quando la variabile dipendente è di tipo dicotomico. L'obiettivo del modello è di stabilire la probabilità con cui un'osservazione può generare uno o l'altro valore della variabile dipendente; può inoltre essere utilizzato per classificare le osservazioni, in base alla caratteristiche di queste, in due categorie.^[1]

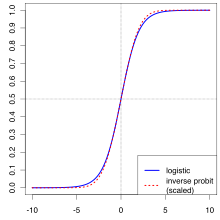
Il modello logit fa parte della classe dei modelli lineari generalizzati, così come il modello probit ed il modello loglineare, dai quali differisce essenzialmente per la scelta della funzione $\Lambda$ .^[1]

Scelta della funzione

La funzione logit. L'inversa di questa funzione è utilizzata nella regressione logistica.

Un modello di regressione dove la variabile dipendente è dicotomica, ossia una variabile che può avere come unici valori 0 e 1 o riconducibili ad essi, calcola la probabilità che questa variabile acquisisca valore 1. Poiché le probabilità per definizione sono limitate ad un intervallo $C=\left[0,1\right]$ , l'utilizzo di un modello di regressione lineare non sarebbe appropriato, infatti esso restituirebbe dei valori appartenenti all'intero insieme $\mathbb {R}$ .^[2] Si supponga infatti il seguente modello lineare:

\Pr(Y=1\mid X=x)=\beta _{0}+\beta _{1}X.

La derivata

{\frac {\partial }{\partial X}}\Pr(Y=1\mid X=x)=\beta _{1}

essendo costante e uguale al parametro $\beta _{1}$ , non permette alla funzione di cambiare pendenza in base al valore di $X$ e quindi di poter avere come codominio $C$ . Questa caratteristica è invece posseduta, ad esempio, dalle funzioni di ripartizione.^[2] L'utilizzo infatti di una funzione non lineare permette di avere una derivata prima dipendente da $X$ e quindi in grado di cambiare al variare di questa variabile. Se si considera infatti il seguente modello:

\Pr(Y=1\mid X=x)=F(\alpha _{0}+\alpha _{1}X),

dove la derivata è la seguente

{\frac {\partial }{\partial X}}\Pr(Y=1\mid X=x)=f(\alpha _{0}+\alpha _{1}X)\alpha _{1}.

Si nota come la pendenza della curva ora possa variare al variare di $X$ , potendo quindi possedere un codominio $C$ . Per il modello logit si utilizza come funzione $F$ la funzione di ripartizione della distribuzione logistica standard.^[1]

Definizione

Il modello di regressione logit per la popolazione è:^[1]^[3]

\mathbb {E} [Y\mid \mathbf {X} ]=\Pr(Y=1\mid X_{1},\ldots ,X_{k})=\Lambda (\mathbf {X} ^{T}{\boldsymbol {\beta }})={\frac {e^{\beta _{0}+\beta _{1}X_{1}+\ldots +\beta _{k}X_{k}}}{1+e^{\beta _{0}+\beta _{1}X_{1}+\ldots +\beta _{k}X_{k}}}}=p,

dove:

$\Pr$ indica la probabilità;
$Y$ è la variabile dipendente dicotomica con una distribuzione bernoulliana $Y\sim {\mathcal {B}}(p)$ ;
$\mathbf {X}$ è il vettore di variabili indipendenti o regressori $X_{1},\ldots ,X_{k}$ ;
${\boldsymbol {\beta }}$ è il vettore di parametri $\beta _{0},\ldots ,\beta _{k}$ ;
$\Lambda$ è la funzione di ripartizione della distribuzione logistica standard;
$e$ è il numero di Eulero, circa uguale a $2,71828$ .

Varianza

La varianza della variabile dipendente risulta dipendere dal vettore dei regressori $\mathbf {X}$ . Infatti

\mathrm {Var} (Y\mid \mathbf {X} )=\mathbb {E} \left[Y^{2}\mid \mathbf {X} \right]-\mathbb {E} \left[Y\mid \mathbf {X} \right]^{2}=\Lambda (\mathbf {X} ^{T}{\boldsymbol {\beta }})\cdot (1-\Lambda (\mathbf {X} ^{T}{\boldsymbol {\beta }})).

Effetto marginale

L'effetto sulla variabile dipendente $Y$ dato da un cambiamento in un regressore $X_{j}$ , chiamato effetto marginale, è calcolato come la derivata del valore atteso di $Y$ rispetto a $X_{j}$ :

{\frac {\partial }{\partial X_{j}}}\mathbb {E} [Y\mid \mathbf {X} ]={\frac {\partial }{\partial X_{j}}}\Lambda (\mathbf {X} ^{T}{\boldsymbol {\beta }})={\frac {\partial }{\partial X_{j}}}{\frac {e^{\mathbf {X} ^{T}{\boldsymbol {\beta }}}}{1+e^{\mathbf {X} ^{T}{\boldsymbol {\beta }}}}}={\frac {e^{\mathbf {X} ^{T}{\boldsymbol {\beta }}}}{1+e^{\mathbf {X} ^{T}{\boldsymbol {\beta }}}}}\cdot {\frac {1}{1+e^{\mathbf {X} ^{T}{\boldsymbol {\beta }}}}}\cdot \beta _{j},

dove $\beta _{j}$ è il parametro associato al regressore $X_{j}$ .^[1] Per il calcolo della derivata il regressore deve essere continuo.

Illustrazione del metodo

Per ogni osservazione campionaria $i=1,\ldots ,n$ si dispone di una determinazione $Y$ e di $k$ determinazioni $X_{1},\ldots ,X_{k}$ . Il modello cerca una relazione non lineare, utilizzando la funzione di ripartizione della distribuzione logistica standard, tra la variabile dipendente e $k$ variabili indipendenti, stimando il valore dei coefficienti $\beta _{0},\ldots ,\beta _{k}$ tramite il metodo della massima verosimiglianza.^[1]

Stima del modello

Il vettore di parametri ${\boldsymbol {\beta }}$ è di norma stimato con il metodo della massima verosimiglianza, con il quale si ottengono stimatori efficienti, consistenti e distribuiti normalmente nel caso in cui il campione statistico sia abbastanza grande.^[4] Queste proprietà permettono di calcolare il test t su un parametro, il test F nel caso di restrizioni multiple e gli intervalli di confidenza.^[4] Alla stima dei parametri segue la stima della probabilità $p$ .

Funzione di verosimiglianza

Nel modello logit la variabile dipendente $Y$ è dicotomica e con distribuzione $Y\sim {\mathcal {B}}(p)$ . Si consideri un campione di $n$ osservazioni dove ciascuna di esse è identificata con $i=1,\ldots ,n$ . Per la definizione del modello, la probabilità che questa variabile sia 1 per una data osservazione $i$ è

\Pr(Y_{i}=1\mid X_{1i},\ldots ,X_{ki})=\Lambda (\beta _{0}+\beta _{1}X_{1i}+\ldots +\beta _{k}X_{ki})=p_{i},

mentre la probabilità che sia 0 è

\Pr(Y_{i}=0\mid X_{1i},\ldots ,X_{ki})=1-\Lambda (\beta _{0}+\beta _{1}X_{1i}+\ldots +\beta _{k}X_{ki})=1-p_{i}.

La distribuzione di probabilità condizionata per ogni elemento $i$ può essere scritta come

\Pr(Y_{i}=y_{i}\mid X_{1i},\ldots ,X_{ki})=p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}}.

Si considera ora l'intero campione e sia assume che $X_{1i},X_{2i},\ldots ,X_{ki},Y_{i}$ siano indipendenti e identicamente distribuite per ogni osservazione $i$ . Risulta quindi che la distribuzione di probabilità congiunta di $(Y_{1},\ldots ,Y_{n})$ è il prodotto delle probabilità condizionate di ogni osservazione:

{\begin{aligned}\Pr(Y_{1}=y_{1},\ldots ,Y_{n}=y_{n}\mid X_{1i},\ldots ,X_{ki})&=\Pr(Y_{1}=y_{1}\mid X_{11},\ldots ,X_{k1})\cdot \ldots \cdot \Pr(Y_{n}=y_{n}\mid X_{1n},\ldots ,X_{kn})=\\&=p_{1}^{y_{1}}(1-p_{1})^{1-y_{1}}\cdot \ldots \cdot p_{n}^{y_{n}}(1-p_{n})^{1-y_{n}}=\prod _{i=1}^{n}p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}}.\end{aligned}}

Si riprende ora la definizione del modello logit e la si sostituisce al posto di $p_{i}$ , ottenendo quindi la funzione di verosimiglianza^[5]

{\begin{array}{l}{\mathcal {L}}_{\textrm {logit}}(\beta _{0},\ldots ,\beta _{k};Y_{1},\ldots ,Y_{n}\mid X_{1i},\ldots ,X_{ki})=\\\qquad \displaystyle \prod _{i=1}^{n}\left[\Lambda (\beta _{0}+\beta _{1}X_{1i}+\ldots +\beta _{k}X_{ki})\right]^{Y_{i}}\left[1-\Lambda (\beta _{0}+\beta _{1}X_{1i}+\ldots +\beta _{k}X_{ki})\right]^{1-Y_{i}}.\end{array}}

Stima dei parametri

Per calcolare gli stimatori ${\hat {\beta }}_{0},{\hat {\beta }}_{1},\ldots ,{\hat {\beta }}_{k}$ dei parametri $\beta _{0},\beta _{1},\ldots ,\beta _{k}$ risulta conveniente calcolare la funzione di log-verosimiglianza poiché in questo modo si riesce a eliminare la produttoria. Si applica quindi il logaritmo alla funzione di verosimiglianza:

{\begin{array}{l}{\mathcal {l}}_{\textrm {logit}}(\beta _{0},\ldots ,\beta _{k};Y_{1},\ldots ,Y_{n}\mid X_{1i},\ldots ,X_{ki})=\ln {\mathcal {L}}_{\textrm {logit}}(\beta _{0},\ldots ,\beta _{k};Y_{1},\ldots ,Y_{n}\mid X_{1i},\ldots ,X_{ki})\\\qquad \displaystyle =\sum _{i=1}^{n}Y_{i}\ln \left[\Lambda (\beta _{0}+\beta _{1}X_{1i}+\ldots +\beta _{k}X_{ki})\right]+\sum _{i=1}^{n}(1-Y_{i})\ln \left[1-\Lambda (\beta _{0}+\beta _{1}X_{1i}+\ldots +\beta _{k}X_{ki})\right]\end{array}}

Gli stimatori calcolati con il metodo della massima verosimiglianza massimizzano la funzione precedente risolvendo il seguente problema:

\left\{{\hat {\beta }}_{0},{\hat {\beta }}_{1},\ldots ,{\hat {\beta }}_{k}\right\}_{MV}=\arg \max _{\beta _{0},\ldots ,\beta _{k}}{\mathcal {l}}_{\textrm {logit}}(\beta _{0},\ldots ,\beta _{k};Y_{1},\ldots ,Y_{n}\mid X_{1i},\ldots ,X_{ki}).

^[6]

Per semplificare la scrittura consideriamo ${\boldsymbol {\beta }}$ un vettore dei parametri $\beta _{0},\beta _{1},\ldots ,\beta _{k}$ , $\lambda$ la derivata di $\Lambda$ , ossia la funzione di densità di probabilità della distribuzione logistica, e $n$ il numero di osservazioni nel campione. Le condizioni per la massimizzazione sono due: quella di primo ordine dove la derivata prima rispetto ai parametri deve essere posta uguale a zero per trovare i punti estremanti, la seconda invece pone la derivata seconda, sempre rispetto ai parametri, minore di zero per determinare le concavità della funzione e quindi garantire che quelli trovati siano solo punti di massimo:

${\frac {\partial }{\partial {\boldsymbol {\beta }}}}{\mathcal {l}}_{\textrm {logit}}({\boldsymbol {\beta }};\mathbf {y} )=0\Longleftrightarrow \sum _{i=1}^{n}\left\{{\frac {y_{i}-\Lambda (\mathbf {x} _{i}'{\boldsymbol {\beta }})}{\Lambda (\mathbf {x} _{i}'{\boldsymbol {\beta }})\left[1-\Lambda (\mathbf {x} _{i}'{\boldsymbol {\beta }})\right]}}\cdot \lambda (\mathbf {x} _{i}'{\boldsymbol {\beta }})\right\}=0;$
${\frac {\partial ^{2}}{\partial {\boldsymbol {\beta }}\partial {\boldsymbol {\beta '}}}}{\mathcal {l}}_{\textrm {logit}}({\boldsymbol {\beta }};\mathbf {y} )<0.$

Solitamente le soluzioni di queste condizioni non sono semplici da determinare oppure non possono essere trovate affatto, ma per ovviare a questo problema si possono utilizzare dei programmi statistici per computer che, attraverso alcuni algoritmi, trovano delle loro approssimazioni.^[6]

Stima della probabilità

Quando è stato calcolato il vettore ${\boldsymbol {\hat {\beta }}}$ , ossia la stima del vettore dei parametri ${\boldsymbol {\beta }}$ , è possibile procedere alla stima della probabilità $p$ . Per definizione del modello, questa probabilità è anche il valore atteso di $Y$ .

{\hat {p}}={\hat {\mathbb {E} }}\left[Y\mid \mathbf {X} \right]=\Lambda (\mathbf {X} ^{T}{\hat {\boldsymbol {\beta }}})={\frac {e^{\mathbf {X} ^{T}{\hat {\boldsymbol {\beta }}}}}{1+e^{\mathbf {X} ^{T}{\boldsymbol {\hat {\beta }}}}}}.

Note

^ ^a ^b ^c ^d ^e ^f (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 442-443, ISBN 978-1-292-07131-2.
^ ^a ^b (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, p. 437, ISBN 978-1-292-07131-2.
^ Il valore attes
^ ^a ^b (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 441-442, ISBN 978-1-292-07131-2.
^ L'intera derivazione della funzione di verosimiglianza è consultabile alle pagine qui riportate. (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 465-466, ISBN 978-1-292-07131-2.
^ ^a ^b (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 465-466, ISBN 978-1-292-07131-2.

Bibliografia

(EN) Alan Agresti, Categorical Data Analysis, Wiley, 2003, ISBN 978-0-471-36093-3.
(EN) William H. Greene, Econometric Analysis, 4ª ed., Prentice Hall, 1999 [1993], ISBN 978-0-130-13297-0.
(EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, ISBN 978-1-292-07131-2.
(EN) P. McCullagh e John A. Nelder, Generalized Linear Models, 2ª ed., Chapman and Hall/CRC, 1989, ISBN 978-0-412-31760-6.

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file sul regressione logistica

Controllo di autorità	LCCN (EN) sh85078131 · GND (DE) 4230396-5 · BNF (FR) cb13737339z (data) · J9U (EN, HE) 987007536257205171

Portale Economia

Portale Statistica

[Definizione-1] ^ ^a ^b ^c ^d ^e ^f (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 442-443, ISBN 978-1-292-07131-2.

[Scelta_funzione-2] (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, p. 437, ISBN 978-1-292-07131-2.

[3] Il valore attes

[Stimatori-4] (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 441-442, ISBN 978-1-292-07131-2.

[5] L'intera derivazione della funzione di verosimiglianza è consultabile alle pagine qui riportate. (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 465-466, ISBN 978-1-292-07131-2.

[metodo_MV-6] (EN) James H. Stock e Mark W. Watson, Regression with a Binary Dependent Variable, in Introduction to Econometrics, 3ª ed., Pearson, 2015, pp. 465-466, ISBN 978-1-292-07131-2.

[1]

[2]

[3]

[4]

[5]

[6]