Spettroscopia rotazionale
La spettroscopia rotazionale (o spettroscopia a microonde) riguarda la misurazione delle transizioni energetiche tra stati rotazionali quantizzati di molecole in fase gas. Gli spettri delle molecole polari possono essere misurati in assorbimento o in emissione con la spettroscopia a microonde[2] o nell'infrarosso lontano. Generalmente lo spettro rotazionale puro di molecole non polari non può essere osservato con queste tecniche, ma può essere osservato e misurato mediante la spettroscopia Raman.
Viene indicata anche come spettroscopia rotazionale pura per distinguerla dalla spettroscopia roto-vibrazionale dove i livelli energetici rotazionali variano insieme con i cambiamenti energetici vibrazionali, e dalla spettroscopia roto-vibronica (o semplicemente spettroscopia vibronica) dove le variazioni rotazionali, vibrazionali ed elettroniche avvengono contemporaneamente.
Nella spettroscopia rotazionale le molecole vengono classificate in seguito alla loro simmetria in rotatori sferici, lineari e simmetrici. Per questi rotatori possono essere ricavate espressioni analitiche che ne descrivono i termini energetici. Per una quarta categoria, i rotatori asimmetrici, possono essere ricavate espressioni analitiche solo fino al livello J=3, mentre i livelli energetici superiori devono essere valutati usando metodi numerici.
I livelli rotazionali sono ricavati teoricamente considerando le molecole come rotatori rigidi e successivamente applicando termini correttivi per considerare le distorsioni centrifughe, la struttura fine, la struttura iperfine e l'interazione di Coriolis. La comparazione tra gli spettri e le espressioni teoriche fornisce valori numerici dei momenti angolari di inerzia dai quali è possibile, in casi favorevoli, derivare valori accurati degli angoli e delle lunghezze di legame delle molecole. In presenza di un campo elettrostatico è presente l'effetto Stark-Lo Surdo che permette di determinare il momento di dipolo elettrico.
Un'importante applicazione della spettroscopia rotazionale si ha nell'esplorazione della composizione chimica del mezzo interstellare utilizzando i radiotelescopi.
Applicazioni
modificaLa spettroscopia rotazionale è stata inizialmente utilizzata per investigare aspetti fondamentali della fisica molecolare. È uno strumento molto preciso per determinare le strutture molecolari in fase gassosa. Può essere utilizzata per determinare i vincoli alla rotazione interna associata alla rotazione del gruppo metile CH3 rispetto al gruppo C6H4Cl nel clorotoluene (C7H7Cl).[3]
Quando può essere osservata la struttura fine o iperfine, la tecnica fornisce anche informazioni sulla struttura elettronica delle molecole. Molta dell'attuale comprensione della natura delle interazioni molecolari deboli come il legame di Van der Waals, legame a idrogeno e ad alogeno è stata ottenuta mediante spettroscopia rotazionale.
In congiunzione con la radioastronomia, la tecnica riveste un ruolo fondamentale nell'esplorazione della composizione chimica del mezzo interstellare. Le transizioni a microonde sono infatti misurate in laboratorio e confrontate con le emissioni osservate nel mezzo interstellare usando radiotelescopi. NH3 è stata la prima molecola poliatomica stabile a essere identificata nel mezzo interstellare.[4]
La misurazione del monossido di cloro[5] è importante per la chimica atmosferica.
Progetti in corso in astrochimica coinvolgono sia spettroscopia a microonde di laboratorio sia osservazioni fatte utilizzando moderni radiotelescopi come l'Atacama Large Millimeter Array (ALMA).[6] Attualmente sono state identificate più di 200 molecole.
A differenza di risonanza magnetica nucleare (NMR), spettroscopia ultravioletta/visibile e spettroscopia infrarossa, la spettroscopia a microonde non ha ancora trovato una diffusa applicazione in chimica analitica.
Informazioni generali
modificaUna molecola in fase gas è libera di ruotare relativamente a un set di assi ortogonali con orientazione fissa nello spazio o incentrati nel centro di massa della molecola. La rotazione libera non è possibile per molecole in fase liquida o fase solida a causa delle forze intermolecolari. Alla rotazione relativa a ogni asse è associato un set di livelli energetici quantizzati dipendenti dal momento d'inerzia sull'asse e dal numero quantico. Così, per molecole lineari i livelli energetici sono descritti da un unico momento d'inerzia e un solo numero quantico, , che definisce il valore del momento angolare rotazionale.
Per le molecole non lineari che siano rotatori simmetrici ci sono due momenti d'inerzia e l'energia dipende anche da un secondo numero quantico rotazionale, , che definisce il vettore componente del momento angolare rotazionale lungo l'asse di simmetria principale.[7] L'analisi dei dati spettroscopici con le espressioni trattate più avanti permette una determinazione quantitativa dei valori dei momenti d'inerzia. Da questi, possono essere dedotti precisi valori sulla struttura e dimensioni delle molecole.
Per una molecola lineare, l'analisi dello spettro rotazionale permette di ottenere i valori della costante rotazionale[8] e del momento di inerzia della molecola e, note le masse atomiche, possono essere dedotte le lunghezze di legame. Ad esempio, per molecole lineari conoscendo le masse atomiche e i momenti d'inerzia possono essere dedotte direttamente le lunghezze di legame.
Nelle molecole biatomiche questo processo è semplice e diretto. Per molecole lineari con più di due atomi è necessario misurare spettri di due o più isomeri topologici, come 16O12C32S e16O12C34S. Questo permette di istituire un insieme di equazioni simultanee e risolvere il problema delle lunghezze di legame.[9] Va sottolineato che le lunghezze di legame ottenute in questo modo, sono leggermente differenti dalla lunghezza di legame all'equilibrio. Questo poiché bisogna considerare l'energia al punto zero nello stato vibrazionale fondamentale, a cui fanno riferimento gli stati rotazionali, mentre la lunghezza di legame all'equilibrio è riferita al minimo della curva potenziale.
La relazione tra le costanti rotazionali è data da
dove ν è un numero quantico vibrazionale e α è la costante di interazione vibro-rotazionale che può essere calcolata se si riescono a trovare i valori B per due diversi stati vibrazionali.[10]
Per altre molecole, se si riesce a risolvere gli spettri e ad assegnare le singole transizioni, allora si possono dedurre sia la lunghezza sia l'angolo di legame. Quando questo non è possibile, come avviene per la maggior parte dei rotatori asimmetrici, quello che si può fare è associare gli spettri ai tre momenti di inerzia calcolati per una struttura molecolare ipotizzata. Variando la struttura molecolare, si può migliorare la corrispondenza con lo spettro, ottenendo una stima qualitativa della struttura. La sostituzione isotopica è uno strumento di inestimabile valore quando si utilizza questo approccio per la determinazione della struttura molecolare.
Classificazione dei rotatori
modificaIn meccanica quantistica, la rotazione libera di una molecola è quantizzata, cosicché l'energia rotazionale e il momento angolare possono assumere soltanto alcuni valori prefissati, che sono collegati in modo semplice al momento di inerzia, , della molecola. Per ogni molecola ci sono tre momenti di inerzia: , e relativi ai tre assi mutualmente ortogonali A, B, e C con l'origine nel centro di massa del sistema (in questo caso la molecola). La convenzione generale (utilizzata anche in questa voce) è di definirli in modo che: , con l'asse che corrisponde al momento di inerzia minore. Alcuni autori invece definiscono l'asse come l'asse di rotazione di ordine più elevato.
Lo schema dei livelli energetici (e di conseguenza le transizioni rotazionali che si osservano negli spettri) delle molecole è determinato dalla loro simmetria. Un modo conveniente di considerare le molecole è di dividerle in quattro classi, in base alla simmetria delle loro strutture:
- Rotatori sferici: i tre momenti di inerzia devono avere lo stesso valore: . Esempi di rotatori sferici sono gli allotropi del fosforo tetramero (P4), il tetracloruro di carbonio (CCl4), il metano (CH4), il silano (SiH4), l'esafluoruro di zolfo (SF6). Tutte queste molecole appartengono al gruppo puntuale Td o Oh.
- Rotatori lineari: per una molecola lineare i momenti d'inerzia sono definiti da: . Nella maggior parte delle applicazioni viene considerato uguale a zero. Esempi di molecole lineari sono l'ossigeno (O2), l'azoto (N2), il monossido di carbonio (CO), l'anidride carbonica (CO2), il radicale ossidrile OH, l'acido cianidrico (HCN), il solfuro di carbonile (OCS), l'acetilene (HC≡CH). Queste molecole appartengono al gruppo puntuale C∞v o D∞h.
- Rotatori simmetrici: in questa classe due momenti di inerzia devono avere lo stesso valore: o . Per definizione devono avere quindi un asse di simmetria di ordine 3 o superiore. Gli spettroscopisti dividono le molecole in due classi: rotatori simmetrici oblati quando e prolati, quando . Gli spettri appaiono molto differenti tra loro e sono immediatamente riconoscibili. Esempi includono:
- Oblati: benzene, ammoniaca NH3. (L'ammoniaca ha un momento di inerzia IC = 4,4128 × 10−47 kg m2 attorno all'asse di rotazione di ordine tre e momenti IA = IB = 2,8059 × 10−47 kg m2 attorno a ciascun asse perpendicolare all'asse C3. Poiché il momento di inerzia singolo è maggiore degli altri due, la molecola è uno sferoide oblato.)[11]
- Prolati: clorometano CH3Cl, metilacetilene CH3C≡CH
- Rotatori asimmetrici: i tre momenti d'inerzia hanno valori differenti. Esempi di piccole molecole in questa classe possono essere l'acqua o il biossido di azoto (NO2 il cui asse di simmetria di ordine più elevato è un asse di rotazione di livello 2. La maggior parte delle grandi molecole sono rotatori asimmetrici.
Regole di selezione
modificaSpettri a microonde e nel lontano infrarosso
modificaLe transizioni tra stati rotazionali si possono osservare in molecole che hanno un momento di dipolo elettrico.[12][13] Una conseguenza di questa regola è che non si può osservare nessuno spettro a microonde per le molecole centrosimmetriche lineari come l'azoto molecolare, N2, o l'acetilene, HCCH, che sono non polari. Le molecole tetraedriche come il metano, CH4, in cui sono nulli sia il momento di dipolo sia la polarizzabilità isotropica, non dovrebbero possedere uno spettro rotazionale puro, a meno di una distorsione centrifuga; infatti quando la molecola ruota attorno a un asse di simmetria triplice, si crea un piccolo momento di dipolo che consente l'osservazione in microonde di un debole spettro rotazionale.[14]
Per i rotatori simmetrici, la regola di selezione per transizioni rotazionali dipolo-elettrico-permesse è ΔK = 0, ΔJ = ±1. Poiché queste transizioni sono legate all'assorbimento (o emissione) di un singolo fotone con spin unitario, la conservazione del momento angolare implica che il momento angolare della molecola può variare al massimo di una unità.[15] In aggiunta, il numero quantico K è limitato a valori compresi nell'intervallo da +J a -J.[16]
Spettri Raman
modificaNella spettroscopia Raman le molecole sono soggette a transizioni nelle quali un fotone incidente viene assorbito e un fotone diffuso viene emesso. La regola di selezione generale perché queste transizioni siano permesse è che la polarizzabilità deve essere anisotropica, vale a dire che non è la stessa in tutte le direzioni.[17] La polarizzabilità è un tensore 3-dimensionale che può essere rappresentato come un ellissoide. L'ellissoide di polarizzabilità di una molecola simmetrica è infatti sferico, per cui queste molecole non possiedono uno spettro Raman rotazionale. Per tutte le altre molecole si possono osservare linee sia di radiazione Stokes sia anti-Stokes[18] e le intensità sono simili a causa del fatto che molti stati rotazionali sono termicamente popolati.
La regola di selezione per le molecole lineari è ΔJ = 0, ±2. La ragione per il valore 2 è che la polarizzabiltà ritorna allo stesso valore due volte durante una rotazione.[19]
La regola di selezione per una molecola rotatore sferico è
- ΔK = 0
- se K = 0, allora ΔJ = ±2
- se K ≠ 0, allora ΔJ = 0, ±1, ±2
Le transizioni con ΔJ = +1 vengono dette appartenere alla serie R, mentre le transizioni con ΔJ = +2 appartengono alla serie S.[20] Dal momento che le transizioni Raman coinvolgono due fotoni, il momento angolare della molecola può cambiare di due unità.
Unità di misura
modificaLe unità usate per le costanti rotazionali dipendono dal tipo di misura.
Negli spettri agli infrarossi (spettroscopia rotovibrazionale) si utilizza in genere il numero d'onda, in cm−1, il cui simbolo è . Il numero d'onda è il numero di onde presenti in un centimetro, e quindi il reciproco della lunghezza d'onda in cm.
Negli spettri a microonde (spettroscopia rotazionale pura) sono in genere usati i MHz (megahertz) o GHz (gigahertz). La relazione tra le due unità di misura si può ricavare dall'espressione:
dove ν è la frequenza, λ è la lunghezza d'onda e c è la velocità della luce. Ne consegue che
Poiché 1 GHz = 109 Hz, la conversione numerica si può esprimere come
Strutture degli spettri rotazionali
modificaRotatori sferici
modificaLe molecole appartenenti a questa categoria non hanno un momento di dipolo permanente. Uno spettro rotazionale puro non può quindi essere osservato con la spettroscopia di emissione o assorbimento, perché non c'è un momento di dipolo permanente la cui rotazione possa essere accelerata da un campo elettrico o da un fotone incidente. Anche la polarizzabilità è isotropica e quindi le transizioni rotazionali pure non possono essere osservate nemmeno con la spettroscopia Raman.
Ciononostante, le costanti rotazionali possono essere ottenute con la spettroscopia rotovibrazionale. Questo è possibile quando una molecole diventa polare in uno stato vibrazionalmente eccitato. Per esempio la molecola del metano è un rotatore simmetrico, ma la banda dello stretching asimmetrico C-H mostra una struttura fine rotazionale nello spettro infrarosso. Questo spettro è interessante anche perché mostra una chiara evidenza dell'effetto Coriolis nella struttura asimmetrica della banda.
Molecole lineari
modificaIl rotatore rigido è un buon punto di partenza dal quale costruire un modello per la rotazione molecolare. Si assume che gli atomi siano particelle puntiformi con massa connessi mediante legami rigidi. Una molecola lineare giace su un singolo asse e ogni atomo si muove sulla superficie di una sfera intorno al centro di massa. I due gradi di libertà rotazionali corrispondono alle coordinate sferiche θ e φ che descrivono la direzione degli assi molecolari e gli stati quantici sono determinati da due numeri quantici J e M. J definisce il valore del momento angolare rotazionale e M la sua componente su un asse fisso nello spazio, come un campo elettrico o magnetico esterno. In assenza di campi esterni, l'energia dipende solo da J. Sotto le condizioni del modello del rotatore rigido, i livelli energetici rotazionali F(J) della molecola possono essere espressi come:
dove è la costante rotazionale della molecola ed è correlata al momento d'inerzia della molecola. In una molecola lineare il momento di inerzia attorno a un asse perpendicolare all'asse della molecola è unico, cioè , per cui:
Per molecole biatomiche:
dove m1 em2 sono le masse degli atomi e d è la loro distanza.
Le regole di selezione richiedono che durante un'emissione o un assorbimento, il numero quantico rotazionale deve cambiare per valori unitari, cioè . Pertanto la posizione delle linee in uno spettro rotazionale saranno date da
dove denota il livello più basso, mentre si riferisce al livello più alto coinvolto nella transizione.
Il diagramma illustra transizioni rotazionali che soddisfano la regola di selezione =1. Le linee tratteggiate mostrano come queste transizioni descrivono caratteristiche che possono essere osservate sperimentalmente. Transizioni adiacenti sono separate da 2B nello spettro osservato. Per l'asse X dello spettro si possono usare come unità di misura la frequenza o il numero d'onda.
Intensità delle transizioni rotazionali
modificaLa probabilità che una transizione avvenga è il fattore più importante che influenza l'intensità di una riga rotazionale osservata. Questa probabilità è proporzionale alla popolazione dello stato iniziale coinvolto nella transizione. La popolazione di uno stato rotazionale dipende da due fattori.
Il primo è che il numero delle molecole in uno stato eccitato con numero quantico J rispetto al numero di molecole nello stato fondamentale, NJ/N0, è dato dalla distribuzione di Boltzmann:
- ,
dove k è la costante di Boltzmann e T è la temperatura assoluta. Questo fattore decresce all'aumentare di J.
Il secondo fattore è la degenerazione di uno stato rotazionale che è uguale a 2J+1. Questo fattore aumenta all'aumentare di J.
Combinando i due fattori si ottiene:[21]
Il massimo relativo d'intensità si ha intorno a:[22][23]
Distorsione centrifuga
modificaQuando una molecola ruota, la forza centrifuga spinge gli atomi verso l'esterno. Ne consegue che il momento di inerzia della molecola aumenta e così diminuisce la costante rotazionale , calcolata con il modello del rotatore rigido. Per tener quindi conto della distorsione centrifuga, bisogna utilizzare dei termini correttivi all'espressione dei livelli energetici della molecola biatomica:[24]
dove è la costante di distorsione centrifuga.
Perciò le posizioni delle linee per il modo rotazionale diventano
Di conseguenza la spaziatura tra i livelli non è costante, come nell'approssimazione, del rotatore rigido ma diminuisce all'aumentare del numero quantico rotazionale.
Alla base di queste espressioni vi è l'assunzione che la vibrazione molecolare segua il moto armonico semplice. In questa approssimazione la costante centrifuga può essere calcolata come
dove k è la costante di forza vibrazionale. Ne consegue che la relazione tra e è
dove è la frequenza di vibrazione armonica.
Nel caso non armonico, si dovrebbero aggiungere alle espressioni per i livelli energetici e le posizioni delle linee, termini con potenze superiori per J.
Un esempio significativo riguarda lo spettro rotazionale dell'acido fluoridrico, per il quale sono stati presi in considerazione termini fino a [J(J+1)]5.[25]
Ossigeno
modificaIl momento di dipolo elettricolo della molecola di diossigeno, O2, è nullo, ma la molecola è paramagnetica e ha due elettroni spaiati, cosicché sono permesse transizioni di dipolo magnetico che possono essere osservate con la spettroscopia a microonde. Lo spin elettronico unitario ha tre orientazioni spaziali rispetto al vettore momento angolare rotazionale della molecola, K, cosicché ogni livello rotazionale è suddiviso in tre stati, J = K + 1, K, e K - 1, e ogni stato J di questo tripletto di tipo p deriva da una differente orientazione dello spin rispetto al movimento rotazionale della molecola.
La differenza energetica tra due termini successivi di J in ognuno di questi tripletti vale circa 2 cm−1 (60 GHz), con la sola eccezione della differenza J = 1←0 che è di 4 cm−1. Le regole di selezione per le transizioni di dipolo magnetico permettono transizioni tra membri successivi del tripletto (ΔJ = ±1), cosicché per ogni valore del numero quantico K del momento angolare, ci sono due transizioni ammesse. Il nucleo del 16O ha momento di spin nucleare nullo, e pertanto considerazioni di simmetria richiedono che K possa assumere solo valori dispari.[26][27]
Rotatori simmetrici
modificaNei rotatori simmetrici il numero quantico J è associato al momento angolare totale della molecola. Per un dato valore di J ci sono 2J+1 stati degeneri e M può assumere tutti i valori compresi nell'intervallo +J ...0 ... -J. Il terzo numero quantico, K, è associato alla rotazione attorno all'asse principale della molecola. In assenza di un campo elettrico esterno, l'energia rotazionale di un rotatore simmetrico è funzione solo di J e K. Nell'approssimazione del rotatore rigido, l'energia di ogni stato rotazionale è data da:
con e per una molecola "prolata" o per una molecola "oblata".
I numeri d'onda della transizione sono dati da
come nel caso delle molecole lineari.[28] Se si applica una correzione del primo ordine per la distorsione centrifuga, i numeri d'onda transizionali diventano
Il termine in DJK ha l'effetto di rimuovere la degenerazione presente nell'approssimazione del rotatore rigido, con differenti valori di K.[29]
Rotatore asimmetrico
modificaUn rotatore si definisce asimmetrico nel caso in cui , ovvero in assenza di un asse di simmetria molecolare, si perde quindi l'invarianza della componente del momento angolare che giace lungo l'asse di simmetria e con essa la proprietà di commutazione tra essa e l'operatore Hamiltoniano. Questo è fondamentale perché tale commutazione si usa per ricavare soluzione analitiche per le energie dei rotatori più semplici, in questo caso però bisogna ricorrere ad approcci approssimati.
Per descrivere un rotatore asimmetrico si introduce un "grado di asimmetria"(detto parametro di asimmetria di Ray), definito come:
ove , e sono le costanti rotazionali; i valori di sono compresi tra +1 e -1, i quali rappresentano rispettivamente il caso del rotatore oblato e prolato, idealmente un rotatore del tutto asimmetrico possiede pari a zero.Qualitativamente i livelli energetici differiscono da quelli di un rotatore simmetrico in quanto non si ripresenta la dipendenza da , per cui per ogni valore di si ottiene un livello energetico diverso, quindi per un dato sono presenti sottolivelli non degeneri.
L'Hamiltoniano del sistema è:
che si può riscrivere come
dove
funzione del parametro di asimmetria di Ray. La riscrittura si rivela favorevole perché gli autovalori di si possono tabulare in funzione di .
Per determinare tali autovalori si procede considerando le autofunzioni del rotatore asimmetrico ( ) come combinazioni lineari delle autofunzioni del rotatore simmetrico ( ), ovvero
In generale, se si sostituisce nell'equazione di Schroedinger e si moltiplica per la funzione complessa coniugata, si ottiene(in un dominio infinito )
Per costruzione le autofunzioni del rotatore simmetrico sono ortogonali (e si suppone normalizzate) per cui si ottiene un set di equazioni, le cui soluzioni si possono trovare risolvendo il classico problema del determinante secolare, di seguito si riporta il caso particolare del rotatore asimmetrico, in cui le funzioni di base dipendono dai tre noti numeri quantici e sono ortogonali (l'overlap è nullo se ).
La matrice associata al bracket si presenta come una diagonale a blocchi, in cui per ogni saranno presenti righe e colonne dipendenti da . Dalla risoluzione di tali equazioni si ottengono le energie legate ad (che dipendono da , quindi per ogni si avranno livelli) e i coefficienti di espansione.
La molecola d'acqua è un importante esempio di rotatore asimmetrico. Ha un intenso spettro di rotazione puro nell'infrarosso lontano, al di sotto di circa 200 cm−1. Il suo spettro è stato dettagliatamente analizzato.[30]
Struttura di quadrupolo
modificaQuando un nucleo ha numero quantico di spin, I, maggiore di ½ allora ha momento di quadrupolo. In questo caso, l'accoppiamento del momento angolare di spin nucleare con il momento angolare di rotazione causa una separazione dei livelli energetici rotazionali.
Questo effetto è conosciuto come struttura iperfine e i livelli risultanti sono 2I+1 se J è maggiore di I; 2J+1 se J è minore di I. Ad esempio, con 14N (I = 1) nell' HCN, tutti i livelli con J>0 sono suddivisi in tre.
Le energie dei sottolivelli sono proporzionali al momento nucleare di quadrupolo e sono una funzione di F e J, dove F = J+I, J+I-1, ..., 0, ... |J-I|. L'osservazione della struttura fine di quadrupolo permette così di determinare la grandezza del momento nucleare di quadrupolo.[31] Questo è un metodo alternativo all'utilizzo della spettroscopia di risonanza di quadrupolo nucleare.
Le regole di selezione per le transizioni rotazionali diventano:[32]
Effetto Stark e Zeeman
modificaIn presenza di un campo elettrico statico esterno la degenerazione 2J+1 di ogni stato rotazionale è parzialmente rimossa a causa dell'effetto Stark. Per esempio in una molecola lineare ogni livello energetico è diviso in J+1 componenti. La grandezza di queste separazioni dipende dal quadrato della forza del campo elettrico e dal quadrato del momento di dipolo della molecola.[33] Questo permette in via teorica di misurare il valore del momento di dipolo delle molecole con alta precisione. Un esempio è dato dal solfuro di carbonile, OCS, con μ = 0,71521 ± 0,00020 debye. Tuttavia, poiché lo splitting dipende da μ2, l'orientazione del dipolo deve essere dedotta da considerazioni quantomeccaniche.[34]
Una simile rimozione della degenerazione avviene quando molecole paramagnetiche sono poste in un campo magnetico a seguito dell'effetto Zeeman. La maggior parte delle molecole osservate in fase gas sono invece diamagnetiche. Tra le eccezioni sono da segnalare il monossido di azoto, NO, il diossido di azoto, NO2, alcuni ossidi di cloro e il radicale ossidrile. L'effetto Zeeman è stato osservato con il diossigeno, O2.[35]
Spettroscopia rotazionale Raman
modificaTransizioni rotazionali molecolari possono essere osservate mediante spettroscopia Raman. Le transizioni rotazionali sono Raman-permesse per tutte le molecole con polarizzabilità anisotropa, vale a dire per tutte le molecole eccetto i rotatori sferici. Questo significa che transizioni rotazionali di molecole che non hanno momento di dipolo permanente, che non possono essere osservate in assorbimento o emissione, possono essere analizzate mediante scattering in spettroscopia Raman.
Spettri Raman ad alta risoluzione si possono ottenere all'infrarosso con la spettroscopia in trasformata di Fourier. Un esempio è lo spettro del 15N2, in cui l'effetto dello spin nucleare provoca una variazione di intensità dell'ordine 3:1 nelle linee adiacenti. Dai dati si deduce una lunghezza di legame di 109,9985 ± 0,0010 pm.[36]
Strumentazione
modificaGran parte degli spettrometri sono personalizzati dai singoli utenti in funzione delle loro necessità a partire da componenti di serie. La strumentazione può essere classificata a seconda dei suoi principi operativi.
Anche se le transizioni rotazionali possono essere rilevate su una regione molto vasta dello spettro elettromagnetico, ci sono limitazioni fisiche per quanto riguarda la banda operativa degli strumenti che renderebbero estremamente costoso e complesso passare a misurazioni in regioni completamente differenti dello spettro.
Gli strumenti e i principi operativi descritti in seguito sono generalmente appropriati per esperimenti di spettroscopia rotazionale condotti in una gamma di frequenze tra 2 e 24 GHz.
Celle in assorbimento e modulazione Stark
modificaUno spettrometro a microonde può essere costruito in modo semplice usando un sorgente di radiazione a microonde, una cella di assorbimento dove viene posto il campione in fase gassosa e come rivelatore un ricevitore supereterodina. Lo spettro può essere ottenuto facendo variare la frequenza della sorgente mentre si registra l'intensità della radiazione trasmessa. Una semplice sezione della guida d’onda può essere utilizzata come cella di assorbimento. Una importante variante della tecnica che consiste nell'applicazione di una corrente alternata mediante elettrodi nella cella di assorbimento, è comunemente definito modulazione Stark e mediante l'uso di ricevitori a sensibilità di fase permette la modulazione delle frequenze per le transizioni rotazionali aumentando la sensibilità. La spettroscopia in assorbimento permette lo studio di campioni che sono termodinamicamente stabili a temperatura ambiente.
Il primo studio di uno spettro a microonde di una molecola, l'ammoniaca NH3, fu eseguito da Cleeton e Williams nel 1934.[37] Esperimenti successivi sfruttarono potenti fonti di microonde come il Klystron, molte delle quali furono sviluppate per l'utilizzo dei radar nella seconda guerra mondiale. Il numero di esperimenti è aumentato in modo notevole subito dopo la seconda guerra mondiale tanto che nel 1948, Walter Gordy poté preparare una recensione dei risultati contenuti in un centinaio di articoli scientifici.[38]
Versioni commerciali di spettrometri a microonde furono costruite dalla Hewlett-Packard[39] negli anni '70 e largamente utilizzate per la ricerca di base. Attualmente si utilizzano anche spettrometri del tipo Balle-Flygare o in trasformata di Fourier con segnale modulato in frequenza.
Spettroscopia a microonde in trasformata di Fourier
modificaLa base teorica della spettroscopia in trasformata di Fourier[40] è analoga a quella utilizzata nella spettroscopia FT-NMR. Il comportamento del sistema è descritto dalle equazioni di Bloch.
Viene dapprima introdotto un breve impulso a microonde (tipicamente 0-3 microsecondi di durata) in risonanza con una transizione rotazionale. Le molecole che assorbono questa energia sono indotte a ruotare coerentemente in fase con la radiazione incidente. La disattivazione dell'impulso di polarizzazione è seguita dall'emissione di microonde che accompagna la perdita di coerenza dell'insieme molecolare. Questo decadimento libero dell'induzione (FID) avviene in un orizzonte temporale di 1-100 microsecondi.
Dopo il lavoro pionieristico di Dicke e collaboratori negli anni '50,[41] il primo spettrometro FT a microonde fu costruito da Ekkers e Flygare nel 1975.[42]
Spettrometro FT a microonde Balle-Flygare
modificaBalle, Campbell, Keenan e Flygare dimostrarono che la tecnica FTMW (microonde in trasformata di Fourier) può essere applicata a una "cella a spazio vuoto" che comprende una camera a vuoto contenente una cavità ottica di Fabry-Perot.[43] Questa tecnica permette di testare un campione pochi millisecondi dopo che ha subito un rapido raffreddamento a pochi kelvin in seguito all'espansione del getto di gas.
Si trattò di un miglioramento rivoluzionario poiché:
- raffreddando le molecole a bassa temperatura si concentra la loro popolazione nei più bassi livelli rotazionali. In congiunzione con i benefici derivanti dall'utilizzo di una cavità di Fabry-Perot, si è ottenuto un incremento della sensibilità e della risoluzione degli spettrometri insieme con la riduzione della complessità degli spettri osservati;
- è stato possibile isolare e studiare molecole debolmente legate, dato che a tali basse temperature non c'è energia sufficiente per la frammentazione o per dar luogo a reazioni chimiche.
William Klemperer è stato un pioniere nell'utilizzo di questi strumenti per l'esplorazione di interazioni a bassa energia. Mentre una cavità di Fabry-Perot o uno spettrometro a microonde Balle-Flygare possono essere messi in risonanza a ogni frequenza compresa tra 6 e 18 GHz, l'ampiezza della banda per le misure singole è ristretta a circa 18 MHz. Un'interessante animazione illustra il funzionamento di questo strumento, che è oggi molto utilizzato nella spettroscopia a microonde.[44]
Spettrometro a microonde FTMW con segnale modulato in frequenza
modificaAvendo notato che la tecnologia elettronica e la digitalizzazione avevano fatto significativi progressi dopo l'introduzione della spettroscopia a microonde FTMW, B. Pate dell'università della Virginia[45] progettò uno spettrometro[46] che manteneva i progressi introdotti da Balle-Flygare, ma introducendo alcune innovazioni:
- l'impiego di un generatore d'onda ad alta velocità (>40 GS/s) per generare una polarizzazione dell'impulso modulata in frequenza in grado di arrivare a 12 GHz in meno di un microsecondo
- l'uso di un oscilloscopio ad alta velocità (>40 GS/s) per digitalizzare ed elaborare in accordo alla trasformata di Fourier il decadimento libero dell'induzione molecolare.
Il risultato è uno strumento che permette lo studio di molecole debolmente legate, ma che è in grado di funzionare in una larghezza di banda di 12 GHz, enormemente ampliata rispetto agli spettrometri Balle-Flygare. Versioni modificate di questo spettrometro vengono utilizzate da gruppi di ricerca negli Stati Uniti, nel Canada e in Europa.[47][48] La capacità di operare su banda larga di questo strumento è complementare all'alta sensibilità e risoluzione offerta dalla versione di Balle-Flygare.
Note
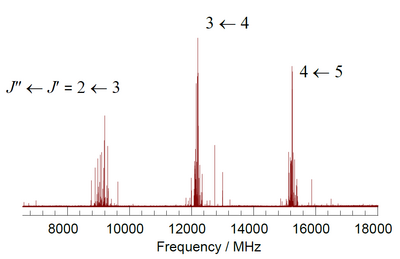
modifica- ^ Spettro ottenuto all'Università di Bristol da misurazioni di oltre due ore tramite trasformata di Fourier a segnale modulato in frequenza nel tempo.
- ^ W. Gordy, Microwave Molecular Spectra in Technique of Organic Chemistry, a cura di A. Weissberger, IX, New York, Interscience, 1970.
- ^ K.P.R. Nair, Demaison, J., Wlodarczak, G. e Merke, I., Millimeterwave rotational spectrum and internal rotation in o-chlorotoluene, in Journal of Molecular Spectroscopy, vol. 237, n. 2, 236, pp. 137–142, Bibcode:2006JMoSp.237..137N, DOI:10.1016/j.jms.2006.03.011.
- ^ A.C. Cheung, Rank, D.M., Townes, C.H., Thornton, D.D. e Welch, W.J., Detection of NH3 molecules in the interstellar medium by their microwave emission spectra, in Physical Review Letters, vol. 21, n. 25, 1968, pp. 1701–5, Bibcode:1968PhRvL..21.1701C, DOI:10.1103/PhysRevLett.21.1701.
- ^ P. Ricaud, Baron, P e de La Noë, J., Quality assessment of ground-based microwave measurements of chlorine monoxide, ozone, and nitrogen dioxide from the NDSC radiometer at the Plateau de Bure, in Ann. Geophys, vol. 22, 2004, pp. 1903–15, Bibcode:2004AnGeo..22.1903R, DOI:10.5194/angeo-22-1903-2004.
- ^ Astrochemistry in Virginia, su virginia.edu. URL consultato il 2 dicembre 2012.
- ^ Atkins de Paula, 2006, p. 444.
- ^ Viene qui utilizzato il linguaggio convenzionale degli spettroscopisti per esprimere la costante rotazionale in cm-1. Pertanto la in questo articolo corrisponde a normalmente utilizzata nella trattazione del rotore rigido.
- ^ Per un rotatore simmetrico, i valori dei due momenti di inerzia possono essere usati per derivare due parametri molecolari. Ogni isotopologo addizionale fornisce informazioni per un ulteriore parametro. Nel caso di un rotatore asimmetrico, da un singolo isotopologo si ottengono informazioni per almeno tre parametri molecolari.
- ^ Banwell McCash, 1994, p. 99.
- ^ I valori dei momenti di inerzia da Atkins de Paula, 2006, p. 445
- ^ Hollas, 1996, p. 95.
- ^ Tali transizioni sono definite transizioni dipolo elettrico permesse. Altre transizioni che coinvolgono quadrupoli, ottupoli, esadecapoli e multipoli superiori possono pure essere permesse, ma l'intensità spettrale è molto più debole, per cui queste transizioni sono difficili da osservare. Transizioni dipolo magnetico permesse avvengono nelle molecole paramagnetiche come il diossigeno, O2, e il monossido di azoto, NO.
- ^ Hollas, 1996, p. 104 riporta parte dello spettro rotazionale del silano.
- ^ Atkins de Paula, 2006, p. 447.
- ^ Banwell McCash, 1994, p. 49.
- ^ Hollas, 1996, p. 111.
- ^ Nella spettroscopia Raman le energie fotoniche per lo scattering Stokes e anti-Stokes sono rispettivamente inferiori e superiori all'energia del fotone incidente.
- ^ Atkins de Paula, 2006, p. 474–5.
- ^ Banwell McCash, 1994, Section 4.2, p. 105, Pure Rotational Raman Spectra.
- ^ Banwell McCash, 1994, p. 40.
- ^ Atkins de Paula, 2006, p. 449.
- ^ Questo valore di J corrisponde al massimo della popolazione considerata come funzione continua di J. Poiché però sono ammessi solo valori interi di J, il picco della linea di intensità si osserva nelle vicinanze dei valori interi di J.
- ^ Banwell McCash, 1994, p. 45.
- ^ D.A. Jennings, Evenson, K.M, Zink, L.R., Demuynck, C., Destombes, J.L., Lemoine, B e Johns,J.W.C., High-resolution spectroscopy of HF from 40 to 1100 cm−1: Highly accurate rotational constants, in Journal of Molecular Spectroscopy, vol. 122, n. 2, aprile 1987, pp. 477–480, Bibcode:1987JMoSp.122..477J, DOI:10.1016/0022-2852(87)90021-X.pdf
- ^ M. W. P. Strandberg, Meng, C. Y. e Ingersoll, J. G., The Microwave Absorption Spectrum of Oxygen, in Phys.Rev., vol. 75, n. 10, 1949, pp. 1524–8, Bibcode:1949PhRv...75.1524S, DOI:10.1103/PhysRev.75.1524.pdf
- ^ Paul H. Krupenie, The Spectrum of Molecular Oxygen (PDF), in J. Phys. Chem. Ref. Data 1, 423 (1972), vol. 1, n. 2, 1972, pp. 423–534, Bibcode:1972JPCRD...1..423K, DOI:10.1063/1.3253101. URL consultato il 15 giugno 2015 (archiviato dall'url originale il 21 dicembre 2016).
- ^ Hollas, 1996, p. 101.
- ^ Hollas, 1996, p. 102 mostra l'effetto sullo spettro a microonde del H3SiNCS.
- ^ Richard T. Hall e Dowling, Jerome M., Pure Rotational Spectrum of Water Vapor, in J. Chem. Phys., vol. 47, n. 7, 1967, pp. 2454–61, Bibcode:1967JChPh..47.2454H, DOI:10.1063/1.1703330. Richard T. Hall e Dowling, Jerome M., Erratum: Pure Rotational Spectrum of Water Vapor, in J. Chem. Phys., vol. 54, n. 11, 1971, p. 4968, Bibcode:1971JChPh..54.4968H, DOI:10.1063/1.1674785.
- ^ James W. Simmons, Anderson, Wallace E. e Gordy,Walter, Microwave Spectrum and Molecular Constants of Hydrogen Cyanide, in Phys. Rev., vol. 77, 1950, pp. 77–79, Bibcode:1950PhRv...77...77S, DOI:10.1103/PhysRev.77.77.
- ^ Raymond Chang, Basic Principles of Spectroscopy, McGraw-Hill, 1971. p139
- ^ Le equazioni per le molecole biatomiche e i rotatori simmetri si possono trovare in Hollas, 1996, p. 102
- ^ Hollas, 1996, p. 102.
- ^ James H. Burkhalter, Roy S. Anderson, William V. Smith e Walter Gordy, The Fine Structure of the Microwave Absorption Spectrum of Oxygen, in Phys. Rev., vol. 79, n. 4, 1950, pp. 651–5, Bibcode:1950PhRv...79..651B, DOI:10.1103/PhysRev.79.651.
- ^ Hollas, 1996, p. 113, illustra lo spettro del 15N2 ottenuto usando la radiazione a 476,5 nm di un laser a argon.
- ^ C.E. Cleeton e Williams, N.H., Electromagnetic waves of 1.1 cm wave-length and the absorption spectrum of ammonia, in Physical Reviews, vol. 45, n. 4, 1934, pp. 234–7, Bibcode:1934PhRv...45..234C, DOI:10.1103/PhysRev.45.234.
- ^ W. Gordy, Microwave spectroscopy, in Reviews of Modern Physics, vol. 20, n. 4, 1948, pp. 668–717, Bibcode:1948RvMP...20..668G, DOI:10.1103/RevModPhys.20.668.
- ^ June 1971, Hewlett Packard Journal (PDF), su hpl.hp.com. URL consultato il novembre 2012 (archiviato dall'url originale il 17 marzo 2017).
- ^ R.H. Schwendemann, Transient Effects in Microwave Spectroscopy, in Ann. Rev. Phys. Chem., vol. 29, 1978, pp. 537–558, Bibcode:1978ARPC...29..537S, DOI:10.1146/annurev.pc.29.100178.002541.
- ^ R.H. Dicke e Romer, R.H., Pulse Techniques in Microwave Spectroscopy, in Rev. Sci. Inst., vol. 26, n. 10, 1955, pp. 915–928, Bibcode:1955RScI...26..915D, DOI:10.1063/1.1715156.
- ^ J. Ekkers e Flygare, W.H., Pulsed microwave Fourier transform spectrometer, in Rev. Sci. Inst., vol. 47, n. 4, 1976, pp. 448–454, Bibcode:1976RScI...47..448E, DOI:10.1063/1.1134647.
- ^ T.J. Balle, Campbell, E.J., Keenan, M.R. e Flygare, W.H., A new method for observing the rotational spectra of weak molecular complexes: KrHCl, in J. Chem. Phys., vol. 72, n. 2, 1980, pp. 922–932, Bibcode:1980JChPh..72..922B, DOI:10.1063/1.439210.
- ^ W. Jager, Balle-Flygare FTMW spectrometer animation (SWF), su chem.ualberta.ca.
- ^ Web page of B.H. Pate Research Group, Department of Chemistry, University of Virginia, su faculty.virginia.edu. URL consultato il novembre 2012 (archiviato dall'url originale il 20 maggio 2017).
- ^ G.G. Brown, Dian, B.C., Douglass, K.O., Geyer, S.M. e Pate, B.H., The rotational spectrum of epifluorohydrin measured by chirped-pulse Fourier transform microwave spectroscopy, in J. Mol. Spectrosc., vol. 238, 2006, pp. 200–212, Bibcode:2006JMoSp.238..200B, DOI:10.1016/j.jms.2006.05.003.
- ^ G.S. Grubbs, Dewberry, C.T., Etchison, K.C., Kerr, K.E. e Cooke, S.A., A search accelerated correct intensity Fourier transform microwave spectrometer with pulsed laser ablation source, in Rev. Sci. Inst., vol. 78, n. 9, 2007, p. 096106, Bibcode:2007RScI...78i6106G, DOI:10.1063/1.2786022.
- ^ D.S. Wilcox, Hotopp, K.M. e Dian, B.C., Two-Dimensional Chirped-Pulse Fourier Transform Microwave Spectroscopy, in J. Phys. Chem. A, vol. 115, n. 32, 2011, pp. 8895–8905, DOI:10.1021/jp2043202.
Bibliografia
modifica- P. W. Atkins e J. de Paula, Molecular Spectroscopy: Section: Pure rotation spectra, in Physical Chemistry, 8th, Oxford University Press, 2006, pp. 431–469, ISBN 0-19-870072-5.
- Colin N. Banwell e Elaine M. McCash, Fundamentals of Molecular Spectroscopy, 4th, McGraw-Hill, 1994, ISBN 0-07-707976-0.
- John M. Brown e Alan Carrington, Rotational spectroscopy of diatomic molecule, Cambridge University Press, 2003, ISBN 0-521-53078-4.
- M. J. Hollas, Modern Spectroscopy[collegamento interrotto], 3rd, Wiley, 1996, ISBN 0-471-96522-7.
- H. W. Kroto, Molecular Rotation Spectroscopy, Dover, 2003, ISBN 0-486-49540-X.
- Donald A. McQuarrie, Quantum Chemistry, University Science Books, 2008, ISBN 1-891389-50-5.
- Charles H. Townes e Arthur L. Schawlow, Microwave Spectroscopy, Dover, 1975, ISBN 978-0-486-61798-5.
- István Kovács, Rotational Structure in the Spectra of Diatomic Molecules, Adam Hilger, 1969, ISBN 0-85274-142-1.
- James E. Wollrab, Rotational spectra and molecular structure, Academic Press, 1967, ISBN 1-4831-9485-X.
Collegamenti esterni
modifica- Infrared gas spectra simulator., su spectralcalc.com.
- Hyperphysics article on Rotational Spectrum, su hyperphysics.phy-astr.gsu.edu.
- A list of microwave spectroscopy research groups around the world, su ifpan.edu.pl. URL consultato il 15 giugno 2015 (archiviato dall'url originale il 20 ottobre 2019).