Teorema di Feuerbach

Il teorema di Feuerbach è un teorema di geometria piana relativo alle proprietà del cerchio dei nove punti o cerchio di Feuerbach.

Fig.1 - Il cerchio dei nove punti è tangente all'incerchio e ai tre excerchi.

Fig.2 - La retta di Eulero è la retta rossa che passa per l'ortocentro (blu), il baricentro (arancione) e il circocentro (verde). Il centro del cerchio dei nove punti (rosso), giace sulla retta e a ugual distanza tra l'ortocentro e il circocentro.

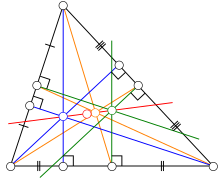
Nel 1822 Karl Feuerbach scoprì che ogni circonferenza dei nove punti di un triangolo è esternamente tangente ai tre excerchi (detti anche cerchi exinscritti) e internamente tangente all'incerchio (o cerchio inscritto), quindi a tutte e quattro le circonferenze tangenti ai tre lati. L'enunciato è:

... la circonferenza che passa per i piedi delle perpendicolari abbassate dai vertici di un qualsiasi triangolo sui lati opposti (altezze), è tangente a tutte le quattro circonferenze che risultano tangenti ai tre lati del triangolo ...

Il punto nel quale il cerchio inscritto nel triangolo e il cerchio dei nove punti si toccano è spesso denominato come punto di Feuerbach.

Feuerbach dimostrò anche che il centro della circonferenza dei nove punti giace sulla retta di Eulero tra l'ortocentro e il circocentro, a ugual distanza da essi (vedi Fig.2), ed inoltre che il Cerchio di Eulero è tangente internamente al cerchio inscritto ed esternamente ai tre cerchi ex-inscritti.

Attribuzione

Fig.3 - Il cerchio dei nove punti.

Sebbene gli venga usualmente accreditato, in realtà Feuerbach non scoprì interamente il cerchio dei nove punti, perché studiò solo sei dei nove punti notevoli. Infatti, nella definizione classica, i nove punti sono: i 3 punti medi dei lati del triangolo, i 3 piedi delle altezze e i 3 punti medi dei segmenti compresi fra i vertici e l'ortocentro. Il fatto che anche questi tre punti appartengono alla stessa circonferenza dei primi sei, non fu analizzato dallo studioso. Inoltre, in una data lievemente precedente, Charles Brianchon e Jean Victor Poncelet avevano enunciato e dimostrato lo stesso teorema. Fu comunque il matematico Olry Terquem, poco dopo Feuerbach, a provare l'esistenza del cerchio dei nove punti. Fu infatti il primo a riconoscere le proprietà dei tre punti medi dei segmenti compresi fra i vertici e l'ortocentro (vedi Fig. 3, punti J, K, e L) e fu quindi il primo a utilizzare il nome "dei nove punti". In tempi successivi si è ulteriormente definito che questa costruzione geometrica contiene diciotto punti rimarchevoli e per questa ragione viene chiamata anche cerchio dei dodici punti, cerchio degli n punti, cerchio medioscritto e cerchio di Eulero.

Voci correlate

• Teoremi di Brianchon

Collegamenti esterni

• (EN) Eric W. Weisstein, Teorema di Feuerbach, su MathWorld, Wolfram Research.