Teorema di Van Kampen

In matematica, e più precisamente in topologia algebrica, il teorema di Seifert-Van Kampen è uno dei principali strumenti per il calcolo del gruppo fondamentale di uno spazio topologico. Venne dimostrato indipendentemente da Herbert Seifert ed Egbert van Kampen agli inizi del 1930.

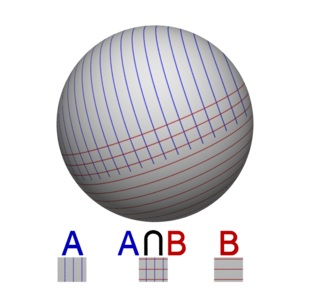
Una sfera è semplicemente connessa, perché si decompone in due calotte aperte $A$ e $B$ semplicemente connesse (sono omeomorfe a $\mathbb {R} ^{2}$ ) con intersezione $A\cap B$ connessa. Questa è una applicazione del teorema di Seifert-Van Kampen. Si noti che l'intersezione *non* è semplicemente connessa: questa non è una ipotesi necessaria per il teorema.

Il teorema afferma che se uno spazio topologico $X$ è unione di due aperti $A$ e $B$ che verifichino certe proprietà di connessione allora la struttura del suo gruppo fondamentale è esprimibile in termini dei gruppi fondamentali di $A,B$ e dell'intersezione di $A$ e $B$ . In tal modo il teorema permette di calcolare il gruppo fondamentale di uno spazio complicato partendo da gruppi fondamentali di spazi più semplici.

Enunciato

Sia $X$ uno spazio topologico, unione di due insiemi aperti

X=A\cup B

tali che tutti e tre gli aperti

A,B,A\cap B

siano connessi per archi. Il teorema di Seifert-Van Kampen asserisce il fatto seguente.

Sia $x_{0}$ un punto base in $A\cap B$ . Il gruppo fondamentale di $X$ è il prodotto amalgamato

\pi (X,x_{0})=\pi (A,x_{0})*_{\pi (A\cap B,x_{0})}\pi (B,x_{0})

Descrizione tramite presentazioni

Il prodotto amalgamato può essere descritto concretamente usando le presentazioni.

Se i gruppi fondamentali di $A$ , $B$ e $A\cap B$ sono descritti come presentazioni

\pi (A,x_{0})=\langle G_{A}\ |\ R_{A}\rangle ,

\pi (B,x_{0})=\langle G_{B}\ |\ R_{B}\rangle ,

\pi (A\cap B,x_{0})=\langle G\ |\ R\rangle

allora il gruppo fondamentale di $X$ è descritto dalla presentazione

\pi (X,x_{0})=\langle G_{A}\cup G_{B}\ |\ R_{A}\cup R_{B}\cup R'\rangle

ottenuta affiancando le presentazioni di $A$ e $B$ e aggiungendo delle nuove relazioni $R'$ . Queste nuove relazioni esprimono il fatto che i lacci contenuti sia in $A$ che in $B$ sono in realtà uguali. Per definirle occorre introdurre gli omomorfismi

i_{A}:\pi (A\cap B,x_{0})\rightarrow \pi (A,x_{0}),

i_{B}:\pi (A\cap B,x_{0})\rightarrow \pi (B,x_{0}),

indotti dalle inclusioni

A\cap B\hookrightarrow A,\quad A\cap B\hookrightarrow B.

L'insieme $R'$ è quindi l'insieme delle relazioni del tipo

R'=\{i_{A}(g)i_{B}^{-1}(g)\ |\ g\in G\}.

Ciascuna di queste relazioni può essere letta nel modo seguente:

i_{A}(g)=i_{B}(g).

Casi particolari

L'enunciato generale del teorema si semplifica in alcuni casi. Ad esempio, nel caso in cui l'intersezione sia semplicemente connessa il prodotto amalgamato si riduce ad un prodotto libero fra gruppi. Come sopra, sia $X$ uno spazio topologico, unione di due aperti $A$ e $B$ connessi per archi e con intersezione connessa per archi.

Se l'intersezione $A\cap B$ è semplicemente connessa, il gruppo fondamentale di $X$ è il prodotto libero

\pi (X,x_{0})=\pi (A,x_{0})*\pi (B,x_{0})\,\!

Con il linguaggio delle presentazioni, questo equivale a dire che non compaiono le relazioni aggiunte $R'$ .

Un altro caso utile è quello in cui uno dei due aperti $A,B$ sia semplicemente connesso.

Se l'aperto $B$ è semplicemente connesso, il gruppo fondamentale di $X$ è il quoziente

\pi (X,x_{0})=\pi (A,x_{0})/_{N(i_{*}\pi (A\cap B,x_{0}))}

dove

i_{*}:\pi (A\cap B,x_{0})\to \pi (A,x_{0})\,\!

è l'omomorfismo indotto dall'inclusione e $N(H)$ indica il normalizzato di $H$ , ovvero il più piccolo sottogruppo normale contenente $H$ .

L'enunciato si semplifica ulteriormente se entrambi gli aperti sono semplicemente connessi.

Se gli aperti $A$ e $B$ sono entrambi semplicemente connessi, anche $X$ è semplicemente connesso.

Applicazioni

Sfera

Il teorema di Seifert-Van Kampen può essere usato per calcolare il gruppo fondamentale della sfera $S^{n}$ di dimensione $n>1$ . Siano $p$ e $q$ due punti antipodali nella sfera. I due aperti

A=S^{n}\setminus \{p\},\quad B=S^{n}\setminus \{q\},

ricoprono la sfera e hanno intersezione connessa per archi (perché $n>1$ ). La proiezione stereografica mostra che $A$ e $B$ sono entrambi omeomorfi a $\mathbb {R} ^{n}$ e quindi semplicemente connessi. Per il teorema di Seifert-Van Kampen, la sfera $S^{n}$ è anch'essa semplicemente connessa.

Si noti che non è necessario che l'intersezione di $A$ e $B$ sia semplicemente connessa per ottenere questo risultato. D'altra parte, è necessario che l'intersezione sia connessa: per $n=1$ questa tecnica non funziona e infatti la circonferenza $S^{1}$ non è semplicemente connessa.

Bouquet di circonferenze

Il bouquet di due circonferenze.

Sia $X$ un bouquet di due circonferenze, ovvero l'unione di due circonferenze $A$ e $B$ nel piano che si intersecano in un punto $x_{0}$ .

Le circonferenze $A$ e $B$ si intersecano in un punto, che è semplicemente connesso. I gruppi fondamentali di $A$ e $B$ sono entrambi isomorfi a $\mathbb {Z}$ . Applicando il teorema di Van Kampen a questi due insiemi otterremmo quindi come gruppo fondamentale il prodotto libero

\mathbb {Z} *\mathbb {Z} .

Il procedimento usato non è però del tutto corretto perché $A$ e $B$ non sono aperti. È però possibile sostituire $A$ e $B$ con due loro intorni aperti opportuni in $X$ in modo da rendere questo argomento rigoroso.

Il gruppo fondamentale così ottenuto non è abeliano. Il laccio $ab$ , che si muove prima lungo $a$ e poi lungo $b$ , non è equivalente al laccio $ba$ .

Toro

Il toro,

Il toro $T$ è omeomorfo al prodotto di due circonferenze

T=S^{1}\times S^{1}

ed ha quindi gruppo fondamentale $\mathbb {Z} \times \mathbb {Z}$ . Questo fatto può essere anche verificato con il teorema di Seifert-Van Kampen come segue.

Il toro è lo spazio quoziente di un quadrato rispetto alla relazione di equivalenza che identifica le coppie di punti che stanno su lati opposti.

Il toro può essere rappresentato come spazio quoziente di un quadrato con i lati opposti $a$ e $b$ identificati parallelamente come in figura. Nel toro, i lati $a$ e $b$ diventano due circonferenze. I quattro vertici del quadrato risultano tutti identificati ad un punto $z$ , che è l'intersezione delle circonferenze $a$ e $b$ . Siano $y$ il punto centrale del quadrato e $x_{0}$ un altro punto interno.

Si scelgono gli aperti di $T$ seguenti:

A=T\setminus \{y\},\quad B=T\setminus (a\cup b).

L'aperto $B$ è dato dalla parte interna del quadrato ed è quindi semplicemente connesso. Spingendo i punti di $A$ radialmente verso il bordo del quadrato si costruisce una retrazione di deformazione di $A$ sull'unione $a\cup b$ delle due circonferenze. Quindi il gruppo fondamentale di $A$ è il gruppo di un bouquet di due circonferenze. Risulta:

\pi (A)=\mathbb {Z} *\mathbb {Z} =\langle x,y\rangle ,

\pi (B)=\{e\},

\pi (A\cap B)=\mathbb {Z} =\langle c\rangle .

L'intersezione $A\cap B$ è infatti omeomorfa ad un quadrato senza un punto, ed il suo gruppo fondamentale è generato dal laccio $c$ mostrato in figura. A questo punto il teorema di Seifert-Van Kampen asserisce che

\pi (T)=\langle x,y\ |\ R\rangle

con

R=\{i_{A}(c)i_{B}(c)^{-1}\}.

Sia $d$ un arco da $x_{0}$ in $z$ come in figura. I generatori $x$ e $y$ di $\pi (T,x_{0})$ sono rappresentati dai lacci $dad^{-1}$ e $dbd^{-1}$ rispettivamente. Il laccio $c$ è omotopo in $A$ a $daba^{-1}b^{-1}d^{-1}$ e quindi si ottiene

i_{A}(c)=daba^{-1}b^{-1}d^{-1}=(dad^{-1})(dbd^{-1})(da^{-1}d^{-1})(db^{-1}d^{-1}).

Ne segue che

i_{A}(c)=xyx^{-1}y^{-1},\quad i_{B}(c)=0.

In conclusione

\pi (T)=\langle x,y\ |\ xyx^{-1}y^{-1}\rangle =\mathbb {Z} \times \mathbb {Z} .

Il termine $xyx^{-1}y^{-1}$ è un commutatore e sta a indicare la relazione di commutazione $xy=yx$ .

Spazio con gruppo fondamentale ciclico finito

Lo spazio

X

è ottenuto come spazio quoziente di un poligono con

n

lati: i lati del poligono sono tutti identificati.

Il metodo usato per calcolare il gruppo fondamentale del toro può essere generalizzato a qualsiasi spazio topologico $X$ ottenuto identificando i lati di un poligono con $n$ lati.