Teorema di Viviani
Il teorema di Viviani, un teorema della geometria euclidea, afferma che la somma delle tre distanze dai lati di un qualunque punto di un triangolo equilatero è costante, e uguale all'altezza del triangolo[1][2][3]. Prende il nome dal matematico italiano Vincenzo Viviani (1622-1703) che lo dimostrò.
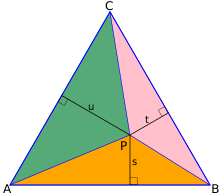
Dimostrazione
modificaLa dimostrazione si basa sul fatto che l'area del triangolo è data dalla regola base per altezza diviso due.
Sia ABC un triangolo equilatero di altezza h e lato a.
Sia P un punto interno del triangolo, e u, s, t le distanze da P dai suoi rispettivi lati. I segmenti che da P incontrano i vertici A, B, and C, suddividono il triangolo ABC in tre triangolini PAB, PBC, and PCA. Poiché il triangolo è equilatero, le loro rispettive basi sono uguali (e costanti) al lato a del triangolo ABC.
Le tre rispettive aree sono , , e . La loro somma fornisce l'area del triangolo. Per cui:
e quindi
- u + s + t = h.
Note
modifica- ^ Una dimostrazione del teorema fu proposta dal matematico Vincenzo Viviani nel 1659.
- ^ (EN) Elias Abboud, On Viviani's Theorem and its Extensions, in College Mathematics Journal, vol. 43, n. 3, 2010, pp. 203-211, DOI:10.4169/074683410X488683.
- ^ Per estensione questa proprietà della somma costante delle distanze di un punto della figura geometrica dai lati appartiene a tutti i poligoni regolari, i poligoni equilateri, i poligoni equiangoli e i poligoni con i lati opposti paralleli.
Bibliografia
modifica- (EN) Elias Abboud, On Viviani's Theorem and its Extensions, in College Mathematics Journal, vol. 43, n. 3, 2010, pp. 203-211, DOI:10.4169/074683410X488683, arXiv:0903.0753.
- (EN) C. Alsina e Roger B. Nelsen, Charming Proofs: A Journey Into Elegant Mathematics, Google books, 2010, p. 96, ISBN 978-0-88385-348-1.
- (EN) Ken-Ichiroh Kawasaki, Yoshihiro Yagi, Katsuya Yanagawa: On Viviani’s Theorem in Three Dimensions. In: The Mathematical Gazette, Vol. 89, No. 515 (Jul., 2005), S. 283–287 (JSTOR 3621243)
- (EN) Hans Samelson: Proof without Words: Viviani’s Theorem with Vectors. In: Mathematics Magazine, Vol. 76, No. 3 (Jun., 2003), S. 225 (JSTOR 3219327)
Altri progetti
modifica- Wikimedia Commons contiene immagini o altri file sul teorema di Viviani
Collegamenti esterni
modifica- (EN) Eric W. Weisstein, Teorema di Viviani, su MathWorld, Wolfram Research.