Teoria di Goldberg

Richard J. Goldberg descrisse matematicamente per la prima volta nel 1952 la reazione antigene-anticorpo che prese inizialmente nome da lui come teoria di Golberg (Goldberg's theory).^[1] Goldberg lavorava nell'Università del Wisconsin; dove predisse che la reazione era governata da fattori statistici, e i risultati sperimentali che forniva erano mostrati in forma grafica. Egli aveva sviluppato una teoria generale per descrivere l'associazione tra un antigene f-valent con un anticorpo bivalente o monovalente.^[2]

Questa teoria di Goldberg è un tentativo di applicare alle reazioni antigene-anticorpo le idee sviluppate da Paul Flory (I936, I941) e Walter H. Stockmayer (I943) in relazione allo studio della polimerizzazione a catena ramificata.^[3]

La teoria di Goldberg prevedeva che l'antigene e l'anticorpo siano immunochimicamente omogenei e che non si verifichino reazioni intra-aggregate che producano complessi ciclici; essendo tutti i legami antigene-anticorpo equivalenti. La teoria fornisce una procedura numerica per il calcolo delle costanti di equilibrio e la costante di velocità delle reazioni antigene-anticorpo e dovrebbe essere utile per il calcolo del comportamento dei sistemi modello.^[4] La teoria di Goldberg è stata un tentativo di applicare idee suggerite dalla teoria dei processi di polimerizzazione a catena ramificata per reazioni Ag-Ab in vitro,^[1] idee derivate dalla teoria della gelificazione di Flory-Stockmayer che è stata la prima teoria a indagare i processi di percolazione^[5]

Successivamente Michael T. Palmiter e Frederick Aladjem (1962) dell'University of Southern California, Los Angeles modificarono la teoria tenendo conto della eterogeneità nella specificità dei siti di legame dell'antigene.^[4]^[6]

Ipotesi

Goldberg immagina due ipotesi:^[1]

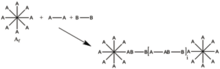
Che le reazioni intra-aggregate che producono strutture cicliche non si verificano in numero apprezzabile, vale a dire che quasi tutti gli aggregati sono costituiti da catene ramificate di Ag alternativo e molecole Ab, senza che nessuna catena formi una ciclizzazione completa.
Che qualsiasi sito che non ha reagito con una molecola Ag o Ab è reattivo come qualsiasi altro sito, indipendentemente dalle dimensioni o dalla forma dell'aggregato (se presente) a cui può trovarsi la molecola già allegata.

Nessun ulteriore presupposto, ad es. sulla natura delle forze di legame o sulle solubilità di aggregati, sono usati nella teoria di Goldberg per calcolare la distribuzione degli aggregati o a fare previsioni sulle precipitazioni. Inoltre, le ipotesi pongono limiti circa la possibile composizione dei singoli aggregati e anche sui possibili stati di massima aggregazione dell'intero sistema.^[1]

Scopo

L'obiettivo originale della teoria era predire gli intervalli e la composizione del precipitato ottenuto dalla reazione Ab-Ag, partendo dalla conoscenza delle sole valenze delle molecole, obiettivo che non si può dire sia riuscito.^[1]

Note

^ ^a ^b ^c ^d ^e Spiers JA, Goldberg's theory of antigen-antibody reactions in vitro., in Immunology, vol. 1, n. 2, 1958, pp. 89-102, ISSN 0019-2805 (WC · ACNP), PMC 1423897, PMID 13538526.
^ Research Report, 1957, pp. 24–.
^ Flory, P.J. (1941). "Molecular Size Distribution in Three Dimensional Polymers I. Gelation". J. Am. Chem. Soc. 63, 3083
^ ^a ^b Michael T. Palmiter e Frederick Aladjem, The antigen-antibody reaction. IV. A quantitative theory of antigen-antibody reactions, in Journal of Theoretical Biology, vol. 5, n. 2, Elsevier BV, 1963, pp. 211-235, DOI:10.1016/0022-5193(63)90060-2, ISSN 0022-5193 (WC · ACNP).
^ Stockmayer, Walter H.(1944). "Theory of Molecular Size Distribution and Gel Formation in Branched Polymers II. General Cross Linking". Journal of Chemical Physics. 12,4, 125
^ Biken's Journal, Research Institute for Microbial Diseases, Osaka University., 1962.

Bibliografia

(EN) J. A. Spiers, Goldberg's Theory of Antigen-Antibody Reactions in Vitro (PDF), su ncbi.nlm.nih.gov, www.ncbi.nlm.nih.gov, 1958, p. 14.
The Journal of Immunology: Official Journal of the American Association of Immunologists, Williams & Wilkins, 1958.
(EN) M. Sahini e M. Sahimi, Applications Of Percolation Theory, CRC Press, 13 luglio 2003, ISBN 978-0-203-22153-2.
(EN) Ivan Kryven, Emergence of the giant weak component in directed random graphs with arbitrary degree distributions, in Physical Review E, vol. 94, n. 1, 27 luglio 2016, p. 012315, DOI:10.1103/PhysRevE.94.012315, ISSN 2470-0045 (WC · ACNP).
Nikolas Morein, Merim Kumars e Gerald Dunders, Microbiologia medica II: sterilizzazione, diagnosi di laboratorio e risposta immunitaria, Cambridge Stanford Books, pp. 225–, GGKEY:TJ4EUUCBTL6.

Voci correlate

Collegamenti esterni

Richard J. Goldberg, A Theory of Antibody—Antigen Reactions. I. Theory for Reactions of Multivalent Antigen with Bivalent and Univalent Antibody2, in Journal of the American Chemical Society, vol. 74, n. 22, American Chemical Society (ACS), 1952, pp. 5715-5725, DOI:10.1021/ja01142a045, ISSN 0002-7863 (WC · ACNP).

Portale Biologia

Portale Chimica

Portale Medicina

[1958_pp._89–102-1] Spiers JA, Goldberg's theory of antigen-antibody reactions in vitro., in Immunology, vol. 1, n. 2, 1958, pp. 89-102, ISSN 0019-2805 (WC · ACNP), PMC 1423897, PMID 13538526.

[2] Research Report, 1957, pp. 24–.

[Flory,_P.J.-3] Flory, P.J. (1941). "Molecular Size Distribution in Three Dimensional Polymers I. Gelation". J. Am. Chem. Soc. 63, 3083

[Palmiter_Aladjem_1963_pp._211–235-4] Michael T. Palmiter e Frederick Aladjem, The antigen-antibody reaction. IV. A quantitative theory of antigen-antibody reactions, in Journal of Theoretical Biology, vol. 5, n. 2, Elsevier BV, 1963, pp. 211-235, DOI:10.1016/0022-5193(63)90060-2, ISSN 0022-5193 (WC · ACNP).

[Stockmayer,_Walter_H.-5] Stockmayer, Walter H.(1944). "Theory of Molecular Size Distribution and Gel Formation in Branched Polymers II. General Cross Linking". Journal of Chemical Physics. 12,4, 125

[6] Biken's Journal, Research Institute for Microbial Diseases, Osaka University., 1962.

[1]

[2]

[3]

[4]

[5]

[6]