Complesso simpliciale

In matematica e in topologia un complesso simpliciale è un'aggregazione ordinata di simplessi, ossia un'unione di un certo numero di simplessi che si intersecano fra loro solo su facce comuni.

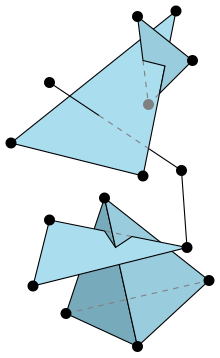
Un complesso simpliciale definisce quindi uno spazio topologico, il quale può essere descritto da più complessi simpliciali differenti, ciascuno dei quali è detto triangolazione dello spazio. Questa descrizione combinatoria permette un calcolo agevole di molte proprietà dello spazio, come il gruppo fondamentale e soprattutto l'omologia. I complessi simpliciali sono quindi un ingrediente fondamentale della topologia algebrica.

Non tutti gli spazi topologici sono però realizzabili come complessi simpliciali.

Definizione

Un complesso simpliciale è un insieme $K$ di simplessi in $\mathbb {R} ^{n}$ tali che:

Ogni faccia di un simplesso in $K$ è un elemento di $K$ .
L'intersezione di due simplessi è vuota o è una faccia di entrambi.
L'insieme $K$ è localmente finito: ogni insieme limitato di $\mathbb {R} ^{n}$ interseca un numero finito di elementi di $K$ .

L'insieme $K$ non è necessariamente finito. La sua dimensione dim $(K)$ è la massima dimensione di un simplesso in $K$ , e non può essere più grande di $n$ .

L'unione dei simplessi è il sostegno o supporto del complesso ed è indicata con $|K|$ . Come sottospazio di $\mathbb {R} ^{n}$ , è uno spazio metrico ed uno spazio topologico.

Chiusura, stella e collegamento

Sia K un complesso simpliciale e sia S una collezione di simplessi in K.

La chiusura di S (denotata Cl S) è il più piccolo sottocomplesso simpliciale di K che contiene ciascun simplesso in S. Cl S si ottiene aggiungendo ripetutamente a S ciascuna faccia di ogni simplesso in S.

La stella di S (denotata St S) è l'insieme di tutti i simplessi in K che hanno una qualsiasi faccia in S. (Si noti che la stella stessa non è generalmente un complesso simpliciale).

Il collegamento di S (denotato Lk S) equivale a Cl St S - St Cl S. È la stella chiusa di S meno le stelle di tutte le facce di S.

Triangolazioni

Politopi

Una triangolazione di un politopo $P$ in $\mathbb {R} ^{n}$ è un complesso simpliciale $K$ il cui supporto è $|K|=P$ . Ad esempio, una triangolazione di un poligono è una suddivisione di questo in triangoli.

Spazi topologici

Una triangolazione di uno spazio topologico $X$ è un complesso simpliciale $K$ tale che $X$ è omeomorfo a $|K|$ .

Uno spazio topologico che ammette una triangolazione è detto triangolabile. Questo è necessariamente di Hausdorff e metrizzabile. Non tutti tali spazi hanno però delle triangolazioni: esistono delle varietà topologiche in dimensione 4 o superiore che non ne hanno. Questo non accade nelle dimensioni inferiori: tutte le varietà di dimensione 1, 2 e 3 sono triangolabili. La triangolabilità è quindi un fattore importante nella topologia della dimensione bassa.

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su complesso simpliciale

Collegamenti esterni

(EN) Eric W. Weisstein, Simplicial Complex, su MathWorld, Wolfram Research.
(EN) Complesso simpliciale, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.

Controllo di autorità	NDL (EN, JA) 00563652

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica