Distribuzione continua uniforme

In teoria delle probabilità la distribuzione continua uniforme è una distribuzione di probabilità continua che è uniforme su un insieme, ovvero che attribuisce la stessa probabilità a tutti i punti appartenenti ad un dato intervallo [a,b] contenuto nell'insieme.

Distribuzione continua uniforme ${\mathcal {U}}(a,b)$ su un intervallo $[a,b]$
Funzione di densità di probabilità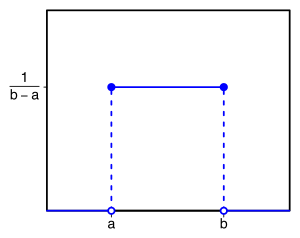
Funzione di ripartizione
Parametri	$a,b\in \mathbb {R}$ $a<b\$
Supporto	$S=[a,b]\$
Funzione di densità	${\frac {1}{b-a}}$ su $S\$
Funzione di ripartizione	${\frac {x-a}{b-a}}$ per $x\in S$
Valore atteso	${\frac {a+b}{2}}$
Mediana	${\frac {a+b}{2}}$
Varianza	${\frac {(b-a)^{2}}{12}}$
Indice di asimmetria	$0$
Curtosi	$-{\frac {6}{5}}$
Entropia	$\log(b-a)\$
Funzione generatrice dei momenti	${\frac {e^{bt}-e^{at}}{bt-at}}$
Funzione caratteristica	${\frac {e^{ibt}-e^{iat}}{ibt-iat}}$

Definizione

La distribuzione continua uniforme ${\mathcal {U}}(S)$ su un insieme misurabile S, di misura finita non nulla, è una distribuzione di probabilità che attribuisce a tutti i sottoinsiemi di S con la stessa misura la stessa probabilità di verificarsi.

La sua densità di probabilità è un multiplo della funzione indicatrice dell'insieme S,

$f(x)={\frac {1}{\mu (S)}}\ 1_{S}={\begin{cases}1/\mu (S)&x\in S\\0&x\not \in S\end{cases}}$

dove $\mu (S)$ è la misura dell'insieme S.

In particolare ogni sottoinsieme misurabile A di S ha una probabilità di verificarsi proporzionale alla propria misura:

$P(A)={\frac {\mu (A)}{\mu (S)}}$.

Su un intervallo

La distribuzione uniforme continua viene solitamente definita su un intervallo $S=[a,b]\subset \mathbb {R}$; in questo caso viene indicata ${\mathcal {U}}(a,b)={\mathcal {U}}([a,b])$.

La sua densità di probabilità è

$f(x)={\frac {1}{b-a}}$ su $[a,b]$.

Come intervallo $[a,b]$, inoltre, viene spesso preso l'intervallo unitario $I=[0,1]$, che può essere sempre ricondotto al caso precedente tramite una trasformazione lineare, ovvero considerando la variabile aleatoria $Y=a+(b-a)X$ al posto di $X$. In particolare, la variabile aleatoria 1-X segue la stessa distribuzione ${\mathcal {U}}(0,1)$.

In questo caso la densità di probabilità diventa

$f(x)=1$ su $I$,

la funzione di ripartizione è

$F(x)=x$ su $I$,

e la probabilità di un intervallo $[x_{1},x_{2}]\subset I$ è pari alla sua lunghezza:

$P([x_{1},x_{2}])=x_{2}-x_{1}\$

(nel caso generale la probabilità di un intervallo è proporzionale alla sua lunghezza).

Per il calcolo delle probabilità i singoli valori f(0) e f(1) sono ininfluenti: basta che la densità di probabilità resti invariata quasi ovunque. Talvolta vengono posti pari a 0, prendendo la funzione indicatrice dell'intervallo aperto $]0,1[$, o a 1/2, prendendo come densità di probabilità la funzione rettangolo (in questo caso la distribuzione è anche chiamata distribuzione rettangolare).

Caratteristiche

Se X è una variabile aleatoria di distribuzione uniforme ${\mathcal {U}}(0,1)$, allora $Y=a+(b-a)X$ è una variabile aleatoria di distribuzione uniforme ${\mathcal {U}}(a,b)$, le cui caratteristiche si ricavano facilmente da quelle di X.

Le due variabili aleatorie hanno

• speranza matematica

$E[X]={\frac {1}{2}},\qquad E[Y]=a+(b-a)E[X]={\frac {a+b}{2}}$;

• varianza

${\text{Var}}(X)={\frac {1}{12}},\qquad {\text{Var}}(Y)=(a-b)^{2}{\text{Var}}(X)={\frac {(a-b)^{2}}{12}}$;

• funzione caratteristica

$\phi _{X}(t)=E[e^{itX}]={\frac {e^{it}-1}{it}},\qquad \phi _{Y}(t)=e^{iat}g_{X}((b-a)t)={\frac {e^{ibt}-e^{iat}}{ibt-iat}}$;

• funzione generatrice dei momenti

$g_{X}(t)=E[e^{tX}]={\frac {e^{t}-1}{t}},\qquad g_{Y}(t)=e^{at}g_{X}((b-a)t)={\frac {e^{bt}-e^{at}}{bt-at}}$;

Dalla funzione generatrice dei momenti si ricavano (per il più generale Y) i momenti semplici

$\mu _{n}(Y)={\frac {b^{n+1}-a^{n+1}}{(n+1)(b-a)}}$;

siccome la variabile aleatoria centrata $Y-E[Y]$ segue una distribuzione uniforme su $[-{\tfrac {b-a}{2}},{\tfrac {b-a}{2}}]$, si ricavano immediatamente i momenti centrali di Y

$m_{n}(Y)=\mu _{n}(Y-E[Y])={\begin{cases}{\frac {(b-a)^{n}}{(n+1)2^{n}}}&n=2k\\0&n=2k+1\end{cases}}.$

In particolare si trovano gli indici di asimmetria e di curtosi

$\gamma _{1}(Y)=0,\qquad \gamma _{2}(Y)=-{\frac {6}{5}}$.

Infine, l'entropia di Y è

$H(Y)=\log(b-a)$.

Altre distribuzioni

Ogni distribuzione di probabilità univariata (cioè sui numeri reali) è legata alla distribuzione uniforme ${\mathcal {U}}(0,1)$. Se X segue la distribuzione uniforme su $[0,1]$ ed F è una qualunque funzione di ripartizione, prendendo la funzione

$F^{-1}(x)=\inf\{y\in \mathbb {R} \colon F(y)\geqslant x\}$

si può definire una variabile aleatoria

$Y=F^{-1}(X)$

che ha proprio F come funzione di ripartizione.

Ad esempio, $Y=-{\tfrac {\log X}{\lambda }}$ segue la distribuzione esponenziale ${\mathcal {E}}(\lambda )$.

In informatica questa proprietà viene chiamata metodo dell'inversione e viene utilizzata per trasformare un generatore "casuale" di campioni per X in un generatore di campioni per Y.

La somma $X_{1}+X_{2}$ di due variabili aleatorie variabili indipendenti con la medesima distribuzione uniforme ${\mathcal {U}}(a,b)$ segue una distribuzione triangolare simmetrica (distribuzione di Simpson).

Più in generale, la distribuzione di Irwin-Hall descrive la somma $X_{1}+...+X_{n}$ di n variabili aleatorie variabili indipendenti con la medesima distribuzione uniforme ${\mathcal {U}}(0,1)$.

La distribuzione Beta $\mathrm {B} (1,1)$ corrisponde alla distribuzione uniforme ${\mathcal {U}}(0,1)$. Inoltre, se X segue questa distribuzione uniforme, allora $Y=1-{\sqrt[{n}]{X}}$ segue la distribuzione Beta $\mathrm {B} (1,n)$.

Il parallelo della distribuzione continua uniforme tra le distribuzioni discrete è la distribuzione discreta uniforme, definita su un insieme finito S, che attribuisce ad ogni suo sottoinsieme una probabilità di verificarsi pari alla propria cardinalità. (In altri termini è la stessa definizione, con una diversa misura.)

Voci correlate

• Distribuzione continua
• Distribuzione discreta uniforme
• Funzione di ripartizione
• Sigma-algebra
• Metodo dell'inversione

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Distribuzione continua uniforme

Collegamenti esterni

• (EN) William L. Hosch, uniform distribution, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Uniform Distribution, su MathWorld, Wolfram Research.
• (EN) Distribuzione continua uniforme, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.

Controllo di autorità	LCCN (EN) sh85038543 · J9U (EN, HE) 987007557954005171