Macchina di Mealy
Nella teoria della calcolabilità, la macchina del Mealy è un automa a stati finiti i cui valori di uscita sono determinati dallo stato attuale e dall'ingresso corrente, a differenza della macchina di Moore, che invece lavora solo in funzione dello stato corrente. Tuttavia, non per tutte le macchine di Mealy si può definire una macchina di Moore equivalente. In quanto il modello di Mealy basa lo stato d'uscita della macchina sia sullo stato in cui si trova, sia sugli input che riceve la macchina, mentre il modello di Moore è valido per le macchine che basano l'output soltanto sullo stato corrente della macchina, indifferentemente dagli input.
L'automa deve il suo nome al suo promotore, lo statunitense G. H. Mealy, che lo descrisse nel trattato A Method for Synthesizing Sequential Circuits nel 1955.
La macchina di Mealy fornisce un rudimentale modello matematico per le macchine cifrate. Utilizzando per l'alfabeto degli ingressi e delle uscite le lettere dell'alfabeto latino, l'automa può lavorare su una data stringa di lettere (ovvero una sequenza di ingressi) che provvede a convertire in una stringa cifrata (ossia una sequenza di uscite). Sebbene sia possibile, ad esempio, descrivere Enigma attraverso una macchina di Mealy, il diagramma degli stati risulterebbe troppo complicato per capire il funzionamento delle macchine cifrate.
Definizione formale
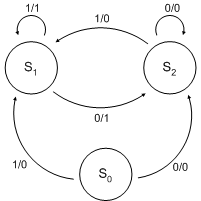
modificaUna macchina di Mealy è una sestupla, {S, S0, Σ, Λ, T, G}, costituita da:
- un insieme finito di stati (S)
- uno stato iniziale S0, che è un elemento di (S)
- un insieme finito chiamato alfabeto degli ingressi ( Σ )
- un insieme finito chiamato alfabeto delle uscite ( Λ )
- una funzione di transizione (T : S × Σ → S)
- una funzione uscita (G : S × Σ → Λ)
Voci correlate
modificaAltri progetti
modifica- Wikimedia Commons contiene immagini o altri file su Macchina di Mealy