Trapezoedro

In geometria per trapezoedro o, impropriamente, deltoedro si intende il poliedro duale di un corrispondente antiprisma. I trapezoedri sono i poliedri duali degli antiprismi, il che significa che, sostituendo vertici con facce e viceversa, si ottengono gli antiprismi equivalenti. Le sue facce sono aquiloni convessi congruenti (detti anche deltoidi). Nessuna delle facce è un trapezoide, quindi il nome trapezoedro, più usato, è fuorviante.

Trapezoedro
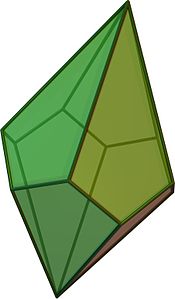Forma facce	aquiloni
Nº facce	2n
Nº spigoli	4n
Nº vertici	2n+2
Valenze vertici	n, 3
Incidenza dei vertici	V3.3.3.n
Notazione di Schläfli	{ } ⨁ {n}
Diagramma di Coxeter-Dynkin
Gruppo di simmetria	Dnd, [2+,2n], (2*n), ordine 4n
Gruppo rotazionale	Dn, [2,n]+, (22n), ordine 2n
Duale	antiprisma n-gonale
Proprietà	non chirale

Il termine deltoedro non va confuso con deltaedro, poliedro con tutte le facce costituite da triangoli equilateri congruenti.

Successione di poliedri

Un trapezoedro ha $2n$ facce. Esiste quindi un trapezoedro per ogni $n>2$. Per $n=3$ il trapezoedro è in realtà un cubo: in questo unico caso gli aquiloni sono dei quadrati, per $n>3$ gli aquiloni sono sempre irregolari.

Costruzione

Il trapezoedro può essere ottenuto da due piramidi a base $n$-gonale regolare congruenti; esse in un primo momento vengono disposte con le basi sovrapposte, poi si sottopone una piramide a una rotazione intorno a suo asse di 180° /$n$ e infine si compenetrano le piramidi e si smussano i loro spigoli di base. Questa costruzione spiega anche perché ci si riferisca ai trapezoedri anche con il nome di antibipiramidi.

Altro modo strettamente analogo di costruire un trapezoedro è considerare due piramidi rette, convesse a base $n$-gonale regolare identiche le cui basi poggino sui $n$-goni regolari identici e congruenti rispetto alle basi di un antiprisma $n$-gonale al centro; l'ipotesi di congruenza delle piramidi rispetto all'antiprisma garantisce la loro rotazione di π/2n sul proprio asse.

Casi particolari

Famiglia dei trapezoedri V.n.3.3.3

Poliedro
Tassellatura
Incidenza	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	...V10.3.3.3	...V12.3.3.3	...V∞.3.3.3

Nel caso particolare del poliedro duale di un antiprisma triangolare, gli aquiloni sono rombi (o quadrati), quindi tali trapezoedri sono anche chiamati zonoedri. Essi si chiamano romboedri e sono cubi deformati secondo la direzione della diagonale del solido; i romboedri sono anche parallelepipedi con facce romboidali congruenti.

Un caso particolare di romboedro è quello le cui facce hanno angoli di 60° e di 120°: tale figura può essere scomposta in due tetraedri regolari uguali e in un ottaedro regolare. Dato che i parallelepipedi possono riempire uno spazio, ne deriva che tale proprietà si estende a un'opportuna combinazione di tetraedri e ottaedri regolari.

Nel caso degenere con n=2, si ha un tetraedro geometrico con 6 vertici, 8 spigoli e facce costituite triangoli derivati da 4 aquiloni degeneri: i duali di tali solidi sono una forma degenerata di antiprismi, ossia altri tetraedri.

Trapezoedro (quadrangolare pentagonale e esagonale): modelli in filo metallico dello scheletro essenziale (vertici e spigoli).

Bibliografia

• H. M. Cundy & A. P. Rollett, I modelli matematici, Milano, Feltrinelli, 1974.
• Maria Dedò, Forme, simmetria e topologia, Bologna, Decibel & Zanichelli, 1999, ISBN 88-08-09615-7.

Voci correlate

• Trapezoedro stellato
• Trapezoedro pentagonale

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «trapezoedro»
• Wikimedia Commons contiene immagini o altri file sul trapezoedro

Collegamenti esterni

• Trapezoedro, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• Ugo Panichi, TRAPEZOEDRO, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1937.
• Trapezoedro, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
• trapezoèdro, su sapere.it, De Agostini.
• (EN) trapezohedron, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Trapezohedron, su MathWorld, Wolfram Research.