Bipiramide triangolare

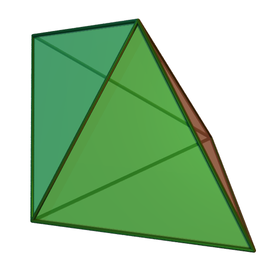
In geometria, la bipiramide triangolare è un esaedro che risulta essere anche il primo elemento di un insieme infinito di bipiramidi transitive per facce.

Bipiramide triangolare
Tipo	Bipiramide Solido di Johnson J11 - J12 - J13
Forma facce	Triangoli
Nº facce	6
Nº spigoli	9
Nº vertici	5
Incidenza dei vertici	V3.4.4
Notazione di Schläfli	{ } + {3}
Diagramma di Coxeter-Dynkin
Gruppo di simmetria	D3h, [3,2], (*223) ordine 12
Gruppo rotazionale	D3, [3,2]+, (223), ordine 6
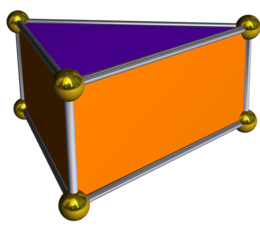
Duale	Prisma triangolare
Proprietà	Convessità, transitivo per facce
Politopi correlati
Poliedro duale
Sviluppo piano

Caratteristiche

Come suggerito dal nome, questo solido con 6 facce, che risulta essere il poliedro duale del prisma triangolare, può essere costruito unendo due tetraedri per una faccia. Sebbene tutte le sue facce siano congruenti ed essa sia transitiva per facce, la bipiramide triangolare non è un solido platonico perché alcuni suoi vertici sono comuni a tre facce e altri a quattro facce.

Nel caso in cui le facce della bipiramide siano tutte triangoli equilateri, allora essa diventa uno dei 92 solidi di Johnson, in particolare il J₁₂. In quanto solido di Johnson, tale bipiramide triangolare è un poliedro convesso e non uniforme e il fatto che le sue facce siano tutte costituite da poligoni regolari la rende un deltaedro, in particolare uno degli otto deltaedri strettamente convessi.

Formule

Considerata una bipiramide triangolare con tutte le facce regolari e con spigolo di lunghezza $L$, le seguenti formule consentono di calcolarne l'altezza $H$, l'area della superficie $A$ e il volume $V$:

$H={\frac {2{\sqrt {6}}}{3}}L\approx 1,632993162\cdot L;$

$A={\frac {3{\sqrt {3}}}{2}}L^{2}\approx 2,598076211\cdot L^{2};$

$V={\frac {\sqrt {2}}{6}}L^{3}\approx 0,235702260\cdot L^{3}.$

Poliedro duale

Il poliedro duale della bipiramide triangolare è, come detto, il prisma triangolare, ossia un prisma con cinque facce: due triangoli equilateri paralleli uniti da una serie di tre rettangoli. Sebbene il prisma triangolare abbia anche una forma che lo rende un poliedro uniforme, ossia quella in cui le sue facce laterali sono quadrati, il poliedro duale della bipiramide triangolare ha le facce laterali rettangolari e non è un poliedro uniforme.

Poliedri e tassellature dello spazio correlati

Come gli altri poliedri, anche la bipiramide triangolare può essere sottoposta a operazione di rettificazione (ossia un troncamento dove gli spigoli sono ridotti della metà), troncamento e levigatura (altrimenti detto anche "addolcimento"). Nella figura sottostante sono rappresentate queste tre operazioni applicate in sequenza al nostro poliedro.

Da sinistra a destra una bipiramide triangolare sottoposta in sequenza a rettificazione, troncamento e levigatura.

La bipiramide triangolare può essere utilizzata per formare una tassellatura dello spazio completa assieme a ottaedri o assieme a tetraedri troncati.

Poliedro aumentato

Bipiramide triangolare costruita aumentando due ottaedri impilati.

La bipiramide triangolare può essere costruita aumentando solidi più piccoli, nella fattispecie due ottaedri regolari impilati con tre bipiramidi triangolari (o sei tetraedri) attorno ai lati e un tetraedro sia sopra che sotto. Il poliedro risultante da tale aumento, che può anche essere creato dall'aumento di una cella di una tassellatura dello spazio tetra-ottaedrica girata, ha 24 facce a forma di triangolo equilatero (4 per faccia), non è un solido di Johnson, avendo esso delle facce complanari, ed è uno degli infiniti casi di deltaedro non strettamente convesso. Si possono generare allo stesso modo poliedri triangolari più grandi, con 9, 16, 25 e più triangoli equilateri per ognuna delle 6 facce, viste come sezione di una tassellatura triangolare.

Proiezione su sfera

La proiezione su una sfera di una bipiramide triangolare sembra la composizione di un osoedro e di un diedro trigonali, ed è membro di una serie infinita di proiezioni su sfera di composti di coppie di poliedri regolari in posizione duale. In associazione con gli altri membri della serie, la bipiramide triangolare è talvolta chiamata "esaedro deltoidale" (o "trapezoidale"), sebbene in essa i "deltoidi" siano dei triangoli e non degli aquiloni.

Mutazione della simmetria *n42 di tassellature duali estese: V3.4.n.4

Simmetria *n32 [n,3]	Sferica				Planare	Iperbolica compatta		Iperbolica paracompatta
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figure Incidenza	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su bipiramide triangolare

Collegamenti esterni

• (EN) Eric W. Weisstein, Bipiramide triangolare, su MathWorld, Wolfram Research.

Bipiramidi regolari n-gonali:

Bipiramide	Bipiramide digonale	Bipiramide triangolare (Vedi: J12)	Bipiramide quadrata (Vedi: O)	Bipiramide pentagonale (Vedi: J13)	Bipiramide esagonale	Bipiramide ettagonale	Bipiramide ottagonale	Bipiramide ennagonale	Bipiramide decagonale	...	Bipiramide apeirogonale
Immagine del poliedro										...
Immagine della tassellatura sferica										Immagine della tassellatura del piano
Incidenza	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Diagramma di Coxeter-Dynkin										...